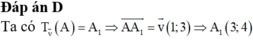Các câu hỏi tương tự
Trong mặt phẳng Oxy, cho điểm A(2;1) và véc tơ
a
→
(1;3). Phép tịnh tiến theo vectơ
a
→
biến điểm A thành điểm A. Tọa độ điểm A là A. (-1;-2) B. (1;2) C. (4;3) D. (3;4)
Đọc tiếp
Trong mặt phẳng Oxy, cho điểm A(2;1) và véc tơ a → (1;3). Phép tịnh tiến theo vectơ a → biến điểm A thành điểm A'. Tọa độ điểm A' là
A. (-1;-2)
B. (1;2)
C. (4;3)
D. (3;4)
Trong mặt phẳng Oxy, cho điểm A(2;5). Phép tịnh tiến theo vectơ
v
→
(
1
;
2
)
biến điểm A thành điểm nào?
Đọc tiếp
Trong mặt phẳng Oxy, cho điểm A(2;5). Phép tịnh tiến theo vectơ v → = ( 1 ; 2 ) biến điểm A thành điểm nào?
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto v → ( 1 ; 1 ) biến điểm A(0;2) thành A’ và biến điểm B(-2;1) thành B’, khi đó:
A. A’B’ = √5
B. A’B’ = √10
C. A’B’ = √11
D. A’B’ = √12
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto v → =(-3;2) biến điểm A(1;3) thành điểm A’ có tọa độ
A. (1;3)
B. (-4;-1)
C. (-2;5)
D. (-3;5)
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto v → =(-3;2) biến điểm A(1;3) thành điểm A’ có tọa độ
A. (1;3)
B. (-4;-1)
C. (-2;5)
D. (-3;5)
Trong mặt phẳng tọa độ Oxy cho điểm A(-1;2) và đường thẳng d có phương trình
3
x
+
y
+
1
0
. Tìm ảnh của A và d.a. Qua phép tịnh tiến theo vectơ v(2;1);b. Qua phép đối xứng trục Oy;c. Qua phép đối xứng qua gốc tọa độ;d. Qua phép quay tâm O góc
90
o
.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho điểm A(-1;2) và đường thẳng d có phương trình 3 x + y + 1 = 0 . Tìm ảnh của A và d.
a. Qua phép tịnh tiến theo vectơ v=(2;1);
b. Qua phép đối xứng trục Oy;
c. Qua phép đối xứng qua gốc tọa độ;
d. Qua phép quay tâm O góc 90 o .
Trong mặt phẳng tọa độ Oxy cho vectơ
v
→
-
1
;
2
,
A
3
;
5
,
B
-
1
;
1
và đường thẳng d có phương trình
x
–
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
Trong mặt phẳng tọa độ Oxy cho vectơ
u
→
(
3
;
-
1
)
. Phép tịnh tiến theo vectơ
u
→
biến điểm M(1;-4) thành
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ u → = ( 3 ; - 1 ) . Phép tịnh tiến theo vectơ u → biến điểm M(1;-4) thành
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy cho vectơ u → (3;-1). Phép tịnh tiến theo vectơ u → biến điểm M(1;-4) thành
A. M'(4;-5)
B. M'(-2;-3)
C. M'(3;-4)
D. M'(4;5)