Bài 1:Cho mạch điện có sơ đồ như hình 27.9. Trong đó ampe kế có số chỉ 0,35A, hiệu điện thế giữa hai đầu Đ1 là U12 3,2V và hiệu điện thế giữa hai đầu đèn Đ2 là U23 2,8V. Hãy:a.Cho biết cường độ dòng điện đi qua đèn Đ1 và đi qua đèn Đ2 là bao nhiêu?b. Tính hiệu điện thế U13 giữa hai đầu ngoài cùng của hai đèn Đ1 và Đ2Bài 2: Cho mạch điện có sơ đồ như hình 27.10. Khi công tắc K đóng, ampe kế có số chỉ là I 0,25A; vôn kế có số chỉ U 5,8V, vôn kế V1 có chỉ số U1 2,8V a. Tính cường độ dòng điện...
Đọc tiếp
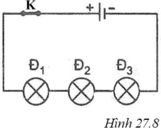
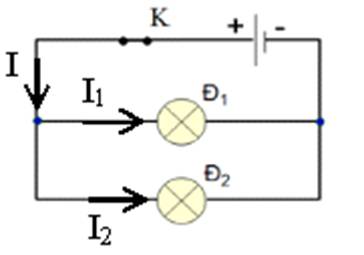
Bài 1:Cho mạch điện có sơ đồ như hình 27.9. Trong đó ampe kế có số chỉ 0,35A, hiệu điện thế giữa hai đầu Đ1 là U12 = 3,2V và hiệu điện thế giữa hai đầu đèn Đ2 là U23 = 2,8V. Hãy:
a.Cho biết cường độ dòng điện đi qua đèn Đ1 và đi qua đèn Đ2 là bao nhiêu?
b. Tính hiệu điện thế U13 giữa hai đầu ngoài cùng của hai đèn Đ1 và Đ2
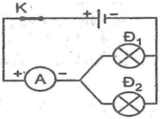
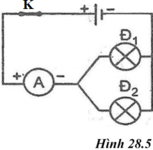
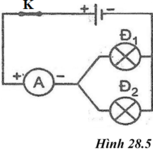
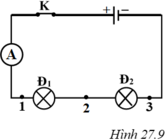
Bài 2: Cho mạch điện có sơ đồ như hình 27.10. Khi công tắc K đóng, ampe kế có số chỉ là I = 0,25A; vôn kế có số chỉ U = 5,8V, vôn kế V1 có chỉ số U1 = 2,8V

a. Tính cường độ dòng điện I1, I2 tương ứng chạy qua các bóng đèn Đ1 và Đ2
b. Tính hiệu điện thế U2 giữa hai đầu bóng đèn Đ2.
c. Độ sáng của đèn sẽ thay đổi như thế nào nếu thay nguồn điện đã cho bằng một nguồn điện khác sao cho số chỉ của vôn kế V là 6V?
Bài 3: Cho mạch điện có sơ đồ như trên hình 27.11, trong đó vôn kế V có chỉ số 6,2V; vôn kế V1 có chỉ số 3,2V. Hãy tính hiệu điện thế giữa hai đầu bóng đèn Đ1 và Đ2