Chọn C
(S) có tâm I (1; -2; 3) và bán kính R = 4
Gọi H là hình chiếu của I lên (P).
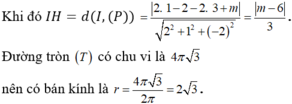
(P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
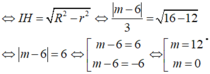
Vậy có 2 giá trị nguyên của m thỏa mãn.
Chọn C
(S) có tâm I (1; -2; 3) và bán kính R = 4
Gọi H là hình chiếu của I lên (P).
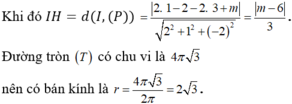
(P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
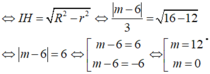
Vậy có 2 giá trị nguyên của m thỏa mãn.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 + 2 x - 4 y - 6 z + m - 3 = 0
Tìm số thực m để β : 2x-y+2z-8=0 cắt (S) theo một đường tròn có chu vi bằng 8 π
A. m = -3
B. m = -4
C. m = -1
D. m = -2
Trong không gian tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 và mặt phẳng (P): x + 2y - 2z - 2 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính là:
A. r = 6
B. r = 2 2
C. r = 4
D. r = 2 3
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) tâm I(1;2;3) và mặt phẳng
(P): 2x - y - 2z + 12 = 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn
có chu vi 6 π . Viết phương trình mặt cầu.
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho mặt phẳng (P): 2x-2y-z-4=0 và mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 11 = 0 . Biết rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn (C). Tọa độ điểm H là tâm đường tròn (C) là:
A. H(3;0;2)
B. H(-1;4;4)
C. H(2;0;3)
D. H(4;4;-1)
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 + 2 x + 4 y - 6 z - m + 4 = 0 . Tìm số thực m để mặt phẳng (P): 2x-2y+z+1=0 cắt (S) theo một đường tròn có bán kính bằng 3.
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho mặt phẳng (P): 2x-y+2z-14=0 và mặt cầu (S): x 2 + y 2 + z 2 - 2 x + 4 y + 2 z - 3 = 0 . Gọi tọa độ điểm M(a;b;c) thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Tính giá trị biểu thức K=a+b+c
A. K=1
B. K=2
C. K=-5
D. K=-2
Trong không gian với hệ tọa độ Oxyz, cho họ đường thẳng (dm): x = 1 + 2 m t y = - 1 + ( 2 m - 1 ) t z = 2 + ( 3 m + 1 ) t , m là tham số thực. Mặt phẳng (a) luôn qua (dm). Tìm chu vi đường tròn giao tuyến của mặt cầu ( S ) : x 2 + y 2 + z 2 - 4 x - 2 y - 2 z - 3 = 0 và mặt phẳng a
A. 2 2
B. 4 2
C. 8 π 66 11
D. 4 2 π
Trong không gian với hệ tọa độ Oxyz, cho ( a ) : 2 x − 2 y − z + 14 = 0 , mặt cầu ( S ) : x 2 + y 2 + z 2 − 2 x − 4 y − 6 z − 11 = 0 . Mặt phẳng (P)//(a) cắt (S) theo thiết diện là một hình tròn có diện tích 16 π . Khi đó phương trình mặt phẳng (P) là
A. 2 x − 2 y − z + 14 = 0
B. 2 x − 2 y − z + 4 = 0
C. 2 x − 2 y − z + 16 = 0
D. 2 x − 2 y − z − 4 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 = 9 và điểm M(1;-1;1). Mặt phẳng (P) đi qua M và cắt (S) theo giao tuyến là đường tròn có chu vi nhỏ nhất có phương trình là:
A. x - y + z - 1 = 0
B. 2x - y - 3z = 0
C. x - y + z - 3 = 0
D. x + y + z - 1 = 0