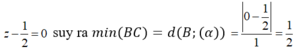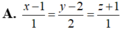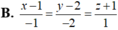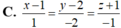Question

Trong không gian với hệ tọa độ Oxyz, xét đường thẳng Δ đi qua điểm A (0;0;1) và vuông góc với mặt phẳng Ozx. Tính khoảng cách nhỏ nhất giữa điểm B (0; 4; 0) tới điểm C trong đó C là điểm cách đều đường thẳng Δ và trục Ox

A. 1/2

B. 3 2

C. 6

D. 65 / 2

Answer 1

Chọn A

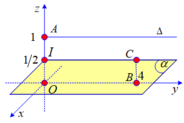
Vì đường thẳng Δ đi qua điểm A (0;0;1) và vuông góc với mặt phẳng Ozx thì Δ song song với trục Oy và nằm trong mặt phẳng Oyz. Dễ thấy OA là đường vuông góc chung của Δ và Ox

Xét mặt phẳng (α) đi qua I (0;0;1/2) và là mặt phẳng trung trực của OA.

Khi đó Δ // (α), Ox // (α) và mọi điểm nằm trên (α) có khoảng cách đến Δ và Ox là bằng nhau.

Vậy tập hợp điểm C là các điểm cách đều đường thẳng Δ và trục Ox là mặt phẳng (α). Mặt phẳng (α) đi qua I (0;0;1/2) có véc tơ pháp tuyến là  nên có phương trình: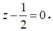

Đoạn BC nhỏ nhất khi C là hình chiếu vuông góc của B lên (α). Do đó khoảng cách nhỏ nhất giữa điểm B (0;4;0) tới điểm C chính là khoảng cách từ B (0;4;0) đến mặt phẳng (α):