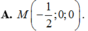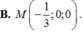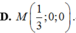Đáp án C
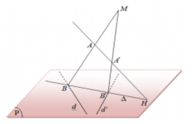
Ta có: M ∈ ( P )
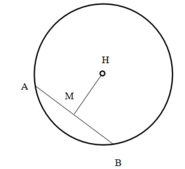
O M 2 = 6 < R 2 = 9 ⇒ M nằm trong mặt cầu ⇒ (P) cắt mặt cầu thành 1 hình tròn (C)
Gọi H là tâm hình tròn (C)
Để AB nhỏ nhất thì A B ⊥ H M
Vì 
O là tâm mặt cầu và O (0; 0; 0)
Phương trình OH: x = t y = t z = t
![]()
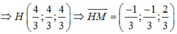
![]() là một vecto chỉ phương của AB
là một vecto chỉ phương của AB
Chọn ![]() là vecto chỉ phương của AB
là vecto chỉ phương của AB
Thì ![]()