Các câu hỏi tương tự
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)CH 3. Trong không gian Oxyz cho 2 vectơ a (1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8CH 4.Trong không...
Đọc tiếp
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (-1; -2; 0), B (0; -4; 0), C (0; 0; -3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A
.
P
:
2
x
-
y
+
3
z
0
B
.
P
:
6
x
-
3
y
+
5
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (-1; -2; 0), B (0; -4; 0), C (0; 0; -3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A . P : 2 x - y + 3 z = 0
B . P : 6 x - 3 y + 5 z = 0
C . P : 2 x - y - 3 z = 0
D . P : - 6 x + 3 y + 4 z = 0
Trong không gian với hệ tọa độ Oxyz, cho A(1 ;-2 ;0), B(0 ;2 ;0), C(2 ;1 ;3). Tọa độ điểm M thỏa mãn
M
A
→
-
M
B
→
+
M
C
→
0
→
là: A. (3;2;-3) B. (3;-2;3) C. (3;-2;-3) D. (3;2;3)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(1 ;-2 ;0), B(0 ;2 ;0), C(2 ;1 ;3). Tọa độ điểm M thỏa mãn M A → - M B → + M C → = 0 → là:
A. (3;2;-3)
B. (3;-2;3)
C. (3;-2;-3)
D. (3;2;3)
Trong không gian với hệ trục tọa độ Oxyz, cho
O
A
→
2
i
→
+
2
j
→
+
2
k
→
, B(-2 ;2 ;0), C(4 ;1 ;-1). Trên mặt phẳng (Oxz) điểm nào dưới đây cách đều ba điểm A, B, C
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho O A → = 2 i → + 2 j → + 2 k → , B(-2 ;2 ;0), C(4 ;1 ;-1). Trên mặt phẳng (Oxz) điểm nào dưới đây cách đều ba điểm A, B, C
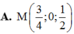

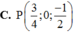
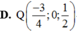
Trong không gian với hệ trục tọa độ Oxyz cho 3 điểm A (1; 1; 1), B (0; 1; 2), C (-2; 1; 4) và mặt phẳng (P): x - y + z + 2 0. Tìm điểm N ∈ (P) sao cho S NA2 + NB2 + NC2 đạt giá trị nhỏ nhất.
A
.
N
-
4
3
;
2
;
4...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho 3 điểm A (1; 1; 1), B (0; 1; 2), C (-2; 1; 4) và mặt phẳng (P): x - y + z + 2 = 0. Tìm điểm N ∈ (P) sao cho S= NA2 + NB2 + NC2 đạt giá trị nhỏ nhất.
A . N - 4 3 ; 2 ; 4 3
B. N (-2; 0; 1)
C . N - 1 2 ; 5 4 ; 3 4
D. N (-1; 2; 1)
Trong không gian với hệ trục tọa độ Oxyz cho A (1; 2; ‒1), B (‒2; 1; 0). Điểm M (a; b; c) thuộc mặt phẳng sao cho . Khi đó giá trị của a bằng?
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho A (1; 2; ‒1), B (‒2; 1; 0). Điểm M (a; b; c) thuộc mặt phẳng sao cho . Khi đó giá trị của a bằng?
![]()
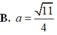
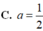

Trong không gian tọa độ Oxyz, cho các điểm A (1; 2; 3), B (2; 1; 0), C (4; 3; -2), D (3; 4; 1), E (1; 1; -1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên? A. 1 B. 4 C. 5 D. Không tồn tại.
Đọc tiếp
Trong không gian tọa độ Oxyz, cho các điểm A (1; 2; 3), B (2; 1; 0), C (4; 3; -2), D (3; 4; 1), E (1; 1; -1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
A. 1
B. 4
C. 5
D. Không tồn tại.
Trong không gian tọa độ Oxyz cho các điểm A(2; 0; 0), A’(6; 0; 0), B(0; 3; 0), B’(0 ;4; 0), C(0; 0; 4), C’(0; 0; 3).
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng: A.
2
B.
6
C. 6 D. 2
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 = 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng:
A. 2
B. 6
C. 6
D. 2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + z -1 0 và điểm A (0; -2; 3), B (2; 0; 1). Điểm M (a; b; c) thuộc (P) sao cho MA + MB nhỏ nhất. Giá trị của a2 + b2 + c2 bằng: A. 41/4 B. 9/4 C. 7/4 D. 3
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + z -1 = 0 và điểm A (0; -2; 3), B (2; 0; 1). Điểm M (a; b; c) thuộc (P) sao cho MA + MB nhỏ nhất.
Giá trị của a2 + b2 + c2 bằng:
A. 41/4
B. 9/4
C. 7/4
D. 3






