Đáp án A
Phương pháp:
Đường thẳng d và d’ có các VTCP lần lượt là u → , v →
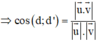
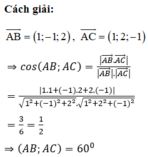
Đáp án A
Phương pháp:
Đường thẳng d và d’ có các VTCP lần lượt là u → , v →
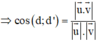
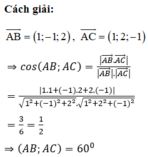
#2H3Y1-2~Trong không gian với hệ tọa độ số Oxyz cho các điểm A(1; 2; 3), B(2; 1; 5), C(2; 4; 2). Góc giữa hai đường thẳng AB và AC bằng:
A. 600
B. 300
C. 1200
D. 1500
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;1;-3), B(1;0;-1) và đường thẳng d : x + 1 2 = y − 2 − 1 = z 1 . Đường thẳng d vuông góc với cả hai đường thẳng AB và d thì có vectơ chỉ phương là vectơ nào trong các vectơ dưới đây?
A. u 1 → = 1 ; − 5 ; 3
B. u 2 → = 1 ; 5 ; 3
C. u 3 → = 4 ; 2 ; 3
D. u 4 → = 3 ; 11 ; 5
Trong không gian với hệ tọa độ Oxyz cho hai điểm A ( 1 ; - 1 ; 1 ) , B ( - 1 ; 2 ; 3 ) và đường thẳng ∆ : x + 1 - 2 = y - 2 1 = z - 3 3 . Phương trình đường thẳng d đi qua điểm A, đồng thời vuông góc với hai đường thẳng AB và Δ là
A. x - 7 1 = y - 2 - 1 = z - 4 1
B. x - 1 7 = y + 1 2 = z - 1 4
C. x + 1 7 = y - 1 - 2 = z + 1 4
D. x + 1 7 = y - 1 2 = z + 1 4
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-4;1;3) và đường thẳng d : x + 1 - 2 = y - 1 1 = z + 3 3 . B là điểm có tọa độ nguyên trên d sao cho A B = 5 . Tìm tọa độ điểm B.
![]()
![]()

![]()
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 x = 1 + t y = 2 - 2 t z = - 3 - t và d 2 x = 4 + 3 t y = 3 + 2 t z = 1 - t . Trên đường thẳng d₁ lấy hai điểm A, B thỏa mã AB=3. Trên đường thẳng d₂ lấy hai điểm C, D thỏa mãn CD=4. Tính thể tích V của tứ diện ABCD.
A. V=7
B. V=2 21
C.V= 4 21 3
D.V= 5 21 6
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d 1 : x - 1 2 = y - 1 - 1 = z + 1 1 , d 2 : x + 2 3 = y + 1 1 = z - 2 2 Đường thẳng đi qua điểm M và cắt cả hai đường thẳng d₁, d₂ tại hai điểm A, B. Độ dài đoạn thẳng AB bằng:
A. √38
B. 2√10
C. 8
D. 12
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;-1), đường thẳng d : x - 1 2 = y + 1 1 = z - 2 - 1 và mặt phẳng (P): x+y+2z+1=0. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. (3;-2;-1)
B. (-3;8;-3)
C. (0;3;-2)
D. (6;-7;0)
Trong không gian tọa độ oxyz, cho mặt cầu (S): (x-1)^2+(y-2)^2+(z+3)^2=6 và hai điểm B(2;3;-1) và C(0;1;-5). Điểm A thuộc mặt cầu (S) sao cho AB<AC. Tia phân giác trong của góc BAC cắt mặt cầu (S) tại K. Hình chiếu của A trên đường thẳng BC là điểm H(a;b;c). Biết AH/AK= căn 15/17, khi đó a+b+c bằng
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 1 - 2 = y - 1 = z - 2 1 và hai điểm A(-1;3;1), B(0;2;-1). Tìm tọa độ điểm C thuộc d sao cho diện tích của tam giác ABC nhỏ nhất.
A. C(-1;0;2)
B. C(1;1;1)
C. C(-3;-1;3)
D. C(-5;-2;4)