Đáp án B
Phương pháp giải:
Tâm đường tròn ngoại tiếp cách đều 3 đỉnh của tam giác và thuộc mặt phẳng chứa tam giác
Lời giải:
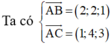
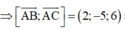
![]()
Vì I(a;b;c) là tâm đường tròn ngoại tiếp tam giác ABC
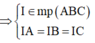
Lại có
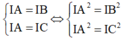
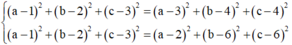
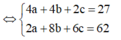
Kết hợp với
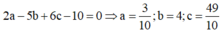
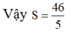
Đáp án B
Phương pháp giải:
Tâm đường tròn ngoại tiếp cách đều 3 đỉnh của tam giác và thuộc mặt phẳng chứa tam giác
Lời giải:
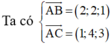
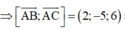
![]()
Vì I(a;b;c) là tâm đường tròn ngoại tiếp tam giác ABC
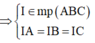
Lại có
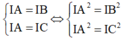
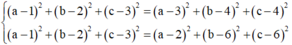
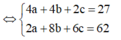
Kết hợp với
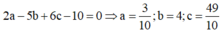
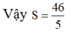
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0;2;-2) và B(2;2;-4). Giả sử I(a;b;c) là tâm đường tròn ngoại tiếp tam giác OAB. Tính a 2 + b 2 + c 2
A. T = 8
B. T = 2
C. T = 6
D. T = 14
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2;2;1), B - 8 3 ; 4 3 ; 8 3 . Biết I(a;b;c) là tâm đường tròn nội tiếp của tam giác OAB. Tính tổng S =a + b + c
A. S = 1
B. S = -1
C. S = 0
D. S = 2
Trong không gian Oxyz cho ba điểm A (1; 2; 3), B (3; 4; 4), C (2; 6; 6) và I (a; b; c) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a + b + c.
A. 63/5
B. 31/3
C. 46/5
D. 10
Trong không gian Oxyz cho các điểm A(5;1;5), B(4;3;2), C(-3;-2;1). Điểm I(a;b;c) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a+2b+c?
A. 1
B. 3
C. 6
D. -9
Trong không gian Oxyz cho các điểm A ( 5 ; 1 ; 5 ) , B ( 4 ; 3 ; 2 ) , C ( - 3 ; - 2 ; 1 ) . Điểm I ( a ; b ; c ) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a + 2 b + c ?
A. 1
B. 3
C. 6
D. - 9
Trong không gian với hệ tọa độ Oxyz, cho A(1;2;3), B(0;-2;1), C(1;0;1). Gọi D là điểm sao cho C là trọng tâm tam giác ABD. Tính tổng các tọa độ của D
A. 1
B. 0
C. 7 3
D. 7
Trong không gian Oxyz, cho tam giác ABC với A(1;0;0), B(0;0;1) và C(2;1;1). Gọi I(a;b;c) là tâm đường tròn ngoại tiếp tam giác. Khi đó a+2b+c bằng
A. 2
B. 4
C. 3
D. 5
Trong không gian Oxyz, cho mặt phẳng α : 2 x + 3 y - 2 z + 12 = 0 . Gọi A, B, C lần lượt là giao điểm của α với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với α có phương trình là
![]()
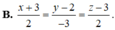
![]()
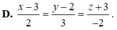
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2x + 3y - 2z + 12= 0. Gọi A, B, C lần lượt là giao điểm của ( α ) với ba trục tọa độ, đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với ( α ) có phương trình là
A. x - 3 2 = y - 2 3 = z - 3 - 2
B. x + 3 2 = y - 2 - 3 = z - 3 2
C. x + 3 2 = y + 2 3 = z - 3 - 2
D. x - 3 2 = y - 2 3 = z + 3 - 2