Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hình chóp có đỉnh S(2;3;5) và đáy là một đa giác nằm trong mặt phẳng P : 2 x + y − 2 z − 3 = 0 , có diện tích bằng 12. Tính thể tích của khối chóp đó.
A. 4
B. 24
C. 8
D. 72
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+y²+ (z+2)²4 và đường thẳng
d
:
x
2
-
y
y
t
z
m
-
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+y²+ (z+2)²=4 và đường thẳng d : x = 2 - y y = t z = m - 1 + t . Gọi T là tập tất cả các giá trị của m để d cắt (S) tại hai điểm phân biệt A, B sao cho các tiếp diện của (S) tại A và B tạo với nhau góc lớn nhất có thể. Tính tổng các phần tử của tập hợp T.
A. 3
B. -3
C. -5.
D. -4.
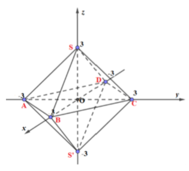
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x-2y+z+50. Gọi giao điểm của mặt phẳng (P) với các trục Ox và Oz lần lượt là X và Z. Tính diện tích OXZ
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x-2y+z+5=0. Gọi giao điểm của mặt phẳng (P) với các trục Ox và Oz lần lượt là X và Z. Tính diện tích OXZ
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng
d
1
:
x
+
1
2
1
-
y
-
m
2
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d 1 : x + 1 2 = 1 - y - m = 2 - z - 3 và d 2 : x - 3 1 = y 1 = z - 1 1 . Tìm tất cả các giá trị thực của m để d 1 ⊥ d 2 được:
A. -1
B. 1
C. -5
D. 5
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) x-y-z+2016=0 và mặt phẳng (Q) x-y-mz=0 . Tất cả các giá trị thực của m để (P)//(Q) là.
A. m=1
B. m=-1
C. m=-2
D. m=2
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng (P): x+y-z-30. Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng
17
2
. Tính bán kính R của mặt cầu (S). A. R3. B. R9 C. R1 D. R5.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng (P): x+y-z-3=0. Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S).
A. R=3.
B. R=9
C. R=1
D. R=5.
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ A(1;2;1), C(3;6;-3). Gọi M là một điểm bất kỳ thuộc mặt cầu
(
S
)
:
x
-
2
2
+
y
-
4
2...
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ A(1;2;1), C(3;6;-3). Gọi M là một điểm bất kỳ thuộc mặt cầu ( S ) : x - 2 2 + y - 4 2 + z + 1 2 = 1 . Tính tổng các khoảng cách từ điểm M đến tất cả các mặt của hình lập phương ABCD.A'B'C'D'.
A. 2 3
B. 3 3
C. 6 3
D. 12
Trong không gian với hệ tọa độ Oxyz cho mặt cầu
S
:
x
-
1
2
+
y
+
1
2
+
z
-
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho mặt cầu S : x - 1 2 + y + 1 2 + z - 2 2 = 16 và điểm A(1;2;3). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba hình tròn tương ứng đó.
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là x²+y²+z²-2x-4y-6z+50. Tính diện tích mặt cầu (S). A. 42π B. 36π C. 9π D. 12π.
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là x²+y²+z²-2x-4y-6z+5=0. Tính diện tích mặt cầu (S).
A. 42π
B. 36π
C. 9π
D. 12π.