Các câu hỏi tương tự
Trong không gian Oxyz, mặt cầu tâm I(1;2;3) đi qua điểm A(1;1;2) có phương trình là: A. (x-1)²+(y-1)²+(z-2)²2 B. (x-1)²+(y-2)²+(z-3)²2 C. (x-1)²+(y-2)²+(z-3)²√2 D. (x-1)²+(y-1)²+(z-2)²√2.
Đọc tiếp
Trong không gian Oxyz, mặt cầu tâm I(1;2;3) đi qua điểm A(1;1;2) có phương trình là:
A. (x-1)²+(y-1)²+(z-2)²=2
B. (x-1)²+(y-2)²+(z-3)²=2
C. (x-1)²+(y-2)²+(z-3)²=√2
D. (x-1)²+(y-1)²+(z-2)²=√2.
Trong không gian Oxyz cho điểm I(2;3;4) và A(1;2;3). Mặt cầu tâm I và đi 2 qua A là A.
(
x
+
2
)
2
+
(
y
+
3
)
2
+
(
z
+
4
)
2...
Đọc tiếp
Trong không gian Oxyz cho điểm I(2;3;4) và A(1;2;3). Mặt cầu tâm I và đi 2 qua A là
A. ( x + 2 ) 2 + ( y + 3 ) 2 + ( z + 4 ) 2 = 3
B. ( x - 2 ) 2 + ( y - 3 ) 2 + ( z - 4 ) 2 = 45
C. ( x + 2 ) 2 + ( y + 3 ) 2 + ( z + 4 ) 2 = 9
D. ( x - 2 ) 2 + ( y - 3 ) 2 + ( z - 4 ) 2 = 3
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là: A. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 B. (x - 2)2 + (y - 2)2 + (z - 1)2 9 và x2 + y2 + (z + 3)2 9 C. (x + 2)2 + (y - 2)2 + (z + 1)2 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 9 D. (x + 1)2 + (y - 2)2 + (z + 2)2 9 và (x - 2)...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng (P): x+ y -z -3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 +
2
. Phương trình mặt cầu (S) là A.
x
+
2
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng (P): x+ y -z -3 =0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + 2 . Phương trình mặt cầu (S) là
A. x + 2 2 + y - 2 2 + z + 1 2 = 9 và x + 1 2 + y - 2 2 + z + 2 2 = 9
B. x - 3 2 + y - 3 2 + z - 3 2 = 9 và x - 1 2 + y - 1 2 + z + 1 2 = 9
C. x + 2 2 + y - 2 2 + z - 1 2 = 9 và x 2 + y 2 + z + 3 2 = 9
D. x + 1 2 + y - 2 2 + z + 2 2 = 9 và x - 2 2 + y - 2 2 + z - 1 2 = 9
Trong không gian Oxyz, cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
3
)
2
48
Gọi...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 48 Gọi ( α ) là mặt phẳng đi qua hai điểm A(0;0-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C). Khối nón (N) có đỉnh là tâm của (S), đường tròn đáy là (C) cỏ thể tích lớn nhất bằng
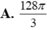
![]()

![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y+1)²+ (z-2)² 16 và điểm A (1;2;3). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó. A. 10π. B. 38 π C. 33 π D. 36 π
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y+1)²+ (z-2)²= 16 và điểm A (1;2;3). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.
A. 10π.
B. 38 π
C. 33 π
D. 36 π
Trong không gian Oxyz cho mặt cầu (S):
(
x
-
2
)
2
+
(
y
-
3
)
2
+
(
z
+
1
)
2
25
đi qua...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu (S): ( x - 2 ) 2 + ( y - 3 ) 2 + ( z + 1 ) 2 = 25 đi qua điểm nào dưới đây.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
1
y
+
2
1
z
1
và mặt phẳng (P): 2x+y-2z+20. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y + 2 1 = z 1 và mặt phẳng (P): 2x+y-2z+2=0. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1, phương trình mặt cầu (S) là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, mặt phẳng đi qua tâm của mặt cầu
(
x
-
1
)
2
+
(
y
+
2
)
2
+
z
2
12
và song song với mặt phẳng (Oxz) có phương trình là: A. y+10. B. y-20. C. y+20...
Đọc tiếp
Trong không gian Oxyz, mặt phẳng đi qua tâm của mặt cầu ( x - 1 ) 2 + ( y + 2 ) 2 + z 2 = 12 và song song với mặt phẳng (Oxz) có phương trình là:
A. y+1=0.
B. y-2=0.
C. y+2=0.
D. x+z-1=0.



