Chọn B
Ta có H (a;b;c) là trực tâm tam giác ABC nên ta có 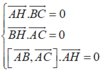

Đường thẳng đi qua trực tâm H (2;1;1) của tam giác ABC và vuông góc với mặt phẳng (ABC) có vecto chỉ phương ![]() có phương trình là
có phương trình là ![]()
Chọn B
Ta có H (a;b;c) là trực tâm tam giác ABC nên ta có 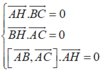

Đường thẳng đi qua trực tâm H (2;1;1) của tam giác ABC và vuông góc với mặt phẳng (ABC) có vecto chỉ phương ![]() có phương trình là
có phương trình là ![]()
Trong không gian Oxyz, cho tam giác ABC với A(3;0;0), B(0;6;0), c(0;0;6). Phương trình nào dưới đây là phương trình đường thắng đi qua trực tâm của tam giác ABC và vuông góc với mặt phẳng (ABC).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A 2 ; 3 ; 1 , B − 1 ; 2 ; 0 , C 1 ; 1 ; − 2 . Đường thẳng d đi qua trực tâm của tam giác ABC và vuông góc với mặt phẳng (ABC) có phương trình là
A. x − 1 1 = y + 5 − 8 = z − 4 5 .
B. x − 2 1 = y + 13 − 8 = z − 9 5 .
C. x + 1 1 = y − 11 − 8 = z + 6 5 .
D. x − 3 1 = y + 21 − 8 = z − 14 5 .
Trong không gian Oxyz, cho tam giác đều ABC với A(6;3;5) và đường thẳng BC có phương trình tham số x = 1 - t y = 2 + t z = 2 t . Gọi ∆ là đường thẳng qua trọng tâm G của tam giác ABC và vuông góc với mặt phẳng (ABC). Điểm nào dưới đây thuộc đường thẳng ∆ ?
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1;0;-1), B (2;3;-1), C (-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
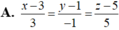
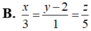
![]()
![]()
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1; 0; -1), B (2; 3; -1), C (-2; 1; 1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
A . x 3 = y - 2 - 1 = z 5
B . x 3 = y - 2 1 = z 5
C . x - 1 1 = y - 2 = z + 1 2
D . x - 3 3 = y - 2 - 1 = z - 5 5
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(0;1;2), B(2;-2;0), C(-2;0;1). Mặt phẳng (P) đi qua A, trực tâm H của tam giác ABC và vuông góc với mặt phẳng ( ABC) có phương trình là
A. 4x + 2y - z + 4 = 0
B. 4x + 2y + z - 4 = 0
C. 4x - 2y - z + 4 = 0
D. 4x - 2y + z + 4 = 0
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A ( 2 ; 1 ; - 2 ) ; B ( 4 ; - 1 ; 1 ) v à C ( 0 ; - 3 ; 1 ) . Phương trình d đi qua trọng tâm của tam giác ABC và vuông góc với mặt phẳng (ABC) là
A. x = 2 + t y = - 1 - 2 t z = - 2 t
B. x = - 2 + t y = - 1 - 2 t z = - 2 t
C. x = 2 + t y = 1 - 2 t z = - 2 t
D. x = 2 + t y = 1 + 2 t z = 2 t
Trong không gian tọa độ Oxy cho tam giác ABC biết A(1;0;-1), B(2;3;-1), C(-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp cảu tam giác ABC và vuông góc với mặt phẳng (ABC).
A. x - 3 3 = y - 1 - 1 = z - 5 5
B. x 3 = y - 2 1 = z 5
C. x - 1 1 = y - 2 = z + 1 2
D. x - 3 3 = y - 2 1 = z 5
Trong không gian Oxyz, cho tam giác ABC với A ( 1 ; - 2 ; 3 ) , B ( - 4 ; 0 ; - 1 ) và C ( 1 ; 1 ; - 3 ) . Phương mặt phẳng (P) đi qua A, trọng tâm G của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
![]()
![]()
![]()
![]()