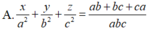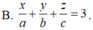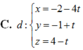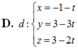Question

Trong không gian Oxyz, cho điểm H (2;1;1). Gọi (P) là mặt phẳng đi qua H và cắt các trục tọa độ tại A, B, C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:

A. 2x + y + z - 6 = 0

B. x + 2y + z - 6 = 0

C. x + 2y + 2z - 6 = 0

D. 2x + y + z + 6 = 0

Answer 1

Chọn A

Cách 1. Giả sử A (a; 0; 0) ∈ Ox, B (0;b;0) ∈ Oy, C (0;0;c) ∈ Oz.

Khi đó mặt phẳng (P) có dạng: 

Do H là trực tâm tam giác ABC nên:

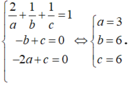
Vậy phương trình của mặt phẳng (P) là: 

Cách 2. Vì tứ diện OABC có các cạnh đôi một vuông tại O và H là trực tâm tam giác ABC nên  (tham khảo bài tập 4, trang 105 SGK HH11).

Suy ra  Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0

H ∈ (P) nên: 2.2 + 1 + 1 + D = 0 => D = -6

Vậy phương trình mặt phẳng  là: 2x + y + z - 6 = 0