Đáp án A
Sử dụng phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng
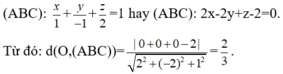
Đáp án A
Sử dụng phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng
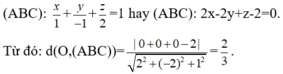
Trong không gian Oxyz, cho bốn điểm A(1;0;0), B(0;-2;0), C(0;0;2), M(1;1;4). Tính khoảng cách từ M đến mặt phẳng (ABC)
A. 0
B. 6 /2
C. 1/2
D. 2
Trong không gian Oxyz, cho ba điểm A(1;0;0), B(0;2;0) và C(0;0;3). Khoảng cách từ gốc tọa độ đến mp (ABC) bằng
A. 3 5
B. 1 3
C. 6 11
D. 6 7
Trong không gian tọa độ Oxyz, cho ba điểm A(1;0;0), B(0;2;0), C(0;0;3). Viết phương trình mặt cầu (S) có tâm là gốc tọa độ O(0;0;0) và tiếp xúc với mặt phẳng (ABC).
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt phẳng (P) đi qua hai điểm A(1;2;3), B(3;-1;1) và song song với đường thẳng d: x - 1 2 = y + 2 - 1 = z - 3 1 . Khoảng cách từ gốc tọa độ đến mặt phẳng bằng
A. 37 101
B. 5 77
C. 37 101
D. 5 77 77
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi tùy ý sao cho a 2 + b 2 + c 2 = 3 . Khoảng cách từ O đến mặt phẳng (ABC) lớn nhất bằng
A. 1 3
B. 3
C. 1 3
D. 1
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(0;-1;2) và N(-1;1;3). Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K(0;0;2) đến mặt phẳng (P) đạt giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến n → của mặt phẳng
A. n → =(1;-1;1)
B. n → =(1;1;-1)
C. n → =(2;-1;1)
D. n → =(2;1;-1)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 2; 4) và B (0; 1; 5). Gọi (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) là lớn nhất. Khi đó, khoảng cách d từ O đến mặt phẳng (P) bằng bao nhiêu?
A . d = - 3 3
B . d = 3
C . d = 1 3
D . d = 1 3
Trong không gian tọa độ Oxyz, cho điểm A(a;b;c) với a , b , c ∈ ℝ \ 0 . Xét (P) là mặt phẳng thay đổi đi qua điểm A. Khoảng cách lớn nhất từ điểm O đến mặt phẳng (P) bằng
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z + 4 = 0 và điểm A(1;-2; 3). Tính khoảng cách từ điểm A đến mặt phẳng (P).
A. 7 3
B. 2
C. 14 2
D. 1