Chọn đáp án A
Gọi M, N lần lượt là trung điểm BC, BD.
Ta có: 
Mà ![]()
Chọn đáp án A
Gọi M, N lần lượt là trung điểm BC, BD.
Ta có: 
Mà ![]()
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt x → = A B → , y → = A C → , z → = A D → . Khẳng định nào sau đây là khẳng định đúng?
A. A G → = 1 3 ( x → + y → + z → )
B. A G → = - 1 3 ( x → + y → + z → )
C. A G → = 2 3 ( x → + y → + z → )
D. A G → = - 2 3 ( x → + y → + z → )
Cho tứ diện ABCD. Gọi A,B',C' lần lượt là trọng tâm các tam giác BCD, ACD, ABD. Đặt A A ' → = a → , B B ' → = b → , C C ' → = c → . Mệnh đề nào sau đây đúng?
![]()
![]()
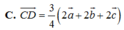
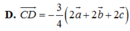
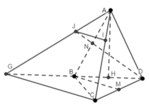
Trong không gian Oxyz, cho tam giác ABC có tọa độ các điểm là: A( x A ; y A , z A ), B( x B ; y B , z B ), C( x C ; y C , z C ). Gọi M là trung điểm của BC, G là trọng tâm tam giác ABC. Khẳng định nào sau đây là sai?
A. M x B + x C 2 ; y B + y C 2 ; z B + z C 2
B. AB → = x B - x A ; y B - y A ; z B - z A
C. G x A + x B + x C 3 ; y A + y B + y C 3 ; z A + z B + z C 3
D. AB = ( x B - x A ) 2 ; y B - y A 2 ; ( z B - z A ) 2
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I ∈ A C , J ∈ D N sao cho IJ // BM. Độ dài IJ theo a là:
A. a 3 3
B. a 2 3
C. a 3 4
D. a 2 2
Cho tứ diện ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm các tam giác BCD và ACD. Trong các khẳng định sau, khẳng định nào sai?
![]()
![]()
![]()
![]()
Cho khối tứ diện ABCD có thể tích 2017. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ.
A. 2017 9
B. 4034 81
C. 8068 27
D. 2017 27
Cho tứ diện ABCD và điểm G thỏa mãn G A → + G B → + G C → + G D → = 0 → (G gọi là trọng tâm của tứ diện). Gọi G A = G A ∩ B C D . Trong các khẳng định sau, khẳng định nào đúng
A. G A → = − 3 G A G →
B. G A → = 4 G A G →
C. G A → = 3 G A G →
D. G A → = 2 G A G →
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
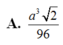
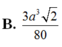
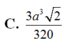
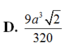
Cho tứ diện ABCD có A B = a ; A C = a 2 ; A D = a 3 các tam giác ABC, ACD, ABD là các tam giác vuông tại đỉnh A. Khoảng cách d từ điểm A đến mặt phẳng (BCD) là
A. d = a 66 11
B. d = a 6 3
C. d = a 30 5
D. d = a 3 2