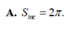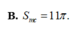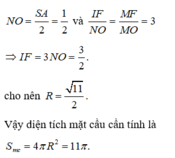Các câu hỏi tương tự
Trong không gian cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với ABBC1, AD2, cạnh bên SA1 và SA vuông góc với đáy. Gọi E là trung điểm AD. Tính diện tích
S
m
c
của mặt cầu ngoại tiếp hình chóp S.CDE.
Đọc tiếp
Trong không gian cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=1, AD=2, cạnh bên SA=1 và SA vuông góc với đáy. Gọi E là trung điểm AD. Tính diện tích S m c của mặt cầu ngoại tiếp hình chóp S.CDE.
![]()
![]()
![]()
![]()
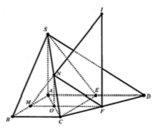
Hình chóp S.ABCD có SA = a là chiều cao của hình chóp và đáy ABCD là hình thang vuông tại A và B có AB = BC = a và AD = 2a. Gọi E là trung điểm của cạnh AD. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.CDE
Cho hình chóp S.ABCD có SA vuông góc với đáy;
S
A
a
6
. Đáy ABCD là hình thang vuông tại A và B,
A
B
B
C
1
2
A
D
a
. Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ECD. A.
R
a
30
3...
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với đáy; S A = a 6 . Đáy ABCD là hình thang vuông tại A và B, A B = B C = 1 2 A D = a . Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ECD.
A. R = a 30 3
B. R = a 19 6
C. R = a 6
D. R = a 114 6
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. AB 1, AD 2 cạnh bên SA vuông góc với đáy và SA
11
.Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. AB = 1, AD = 2 cạnh bên SA vuông góc với đáy và SA= 11 .Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD.
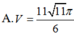
![]()
![]()
![]()
Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCD là hình thang vuông tại A và D, AB 2a, AD CD a, SA 2a. Gọi I là trung điểm của AB. Thể tích của khối cầu ngoại tiếp tứ diện S.AICD là A.
πa
3
6
B.
πa
3
3
C....
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với đáy, ABCD là hình thang vuông tại A và D, AB = 2a, AD = CD = a, SA = 2a. Gọi I là trung điểm của AB. Thể tích của khối cầu ngoại tiếp tứ diện S.AICD là
A. πa 3 6
B. πa 3 3
C. πa 3 5
D. Đáp án khác
Cho hình chóp S.ABCD đáy là hình thang cân có ABCDBCa, AD2a. Cạnh bên SA vuông góc với mặt đáy, SA2a. Tính thể tích khối cầu ngoại tiếp hình chóp S.BCD.
Đọc tiếp
Cho hình chóp S.ABCD đáy là hình thang cân có AB=CD=BC=a, AD=2a. Cạnh bên SA vuông góc với mặt đáy, SA=2a. Tính thể tích khối cầu ngoại tiếp hình chóp S.BCD.
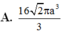
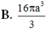
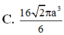
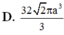
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD 2a, AB BC SA a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD). A. h
a
3
B. h
a
6
6
C. h
a
6
3
D. h
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD = 2a, AB = BC = SA = a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).
A. h = a 3
B. h = a 6 6
C. h = a 6 3
D. h = a 3 6
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết SA
⊥
(ABCD), ABBCa, SAa
2
, AD2a. Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm S, A, B, C, E.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết SA ⊥ (ABCD), AB=BC=a, SA=a 2 , AD=2a. Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm S, A, B, C, E.
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE A.
14
πa
2
B.
11
πa
2
C.
8
πa
2
D.
12
πa
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA = a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE
A. 14 πa 2
B. 11 πa 2
C. 8 πa 2
D. 12 πa 2