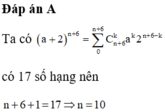Các câu hỏi tương tự
Trong khai triển nhị thức
a
+
2
n
+
6
có tất cả 17 số hạng. Khi đó giá trị n bằng:
Đọc tiếp
Trong khai triển nhị thức a + 2 n + 6 có tất cả 17 số hạng. Khi đó giá trị n bằng:
![]()
![]()
![]()
![]()
Trong khai triển nhị thức Niutơn của a + 2 n + 6 có tất cả 17 số hạng . Khi đó giá trị n bằng
A. 10
B. 11
C. 16
D. 17
Trong khai triển nhị thức
a
+
2
n
+
6
,
n
∈
ℕ
. Có tất cả 17 số hạng. Vậy n bằng: A. 17 B. 11 C. 10 D. 12
Đọc tiếp
Trong khai triển nhị thức a + 2 n + 6 , n ∈ ℕ . Có tất cả 17 số hạng. Vậy n bằng:
A. 17
B. 11
C. 10
D. 12
Trong khai triển nhị thức
(
x
+
2
)
n
+
6
;
(
n
∈
ℕ
)
Có tất cả 17 số hạng. Vậy n bằng A.17. B.11. C.10. D.12.
Đọc tiếp
Trong khai triển nhị thức ( x + 2 ) n + 6 ; ( n ∈ ℕ ) Có tất cả 17 số hạng. Vậy n bằng
A.17.
B.11.
C.10.
D.12.
Trong khai triển nhị thức
(
x
+
2
)
n
+
6
v
ớ
i
n
∈
ℕ
có tất cả 19 số hạng. Vậy n bằng A. 11 B. 12 C. 10 D. 19
Đọc tiếp
Trong khai triển nhị thức ( x + 2 ) n + 6 v ớ i n ∈ ℕ có tất cả 19 số hạng. Vậy n bằng
A. 11
B. 12
C. 10
D. 19
Tìm n
∈
N biết khai triển nhị thức
(
a
+
2
)
n
+
4
,
a
≠
2 có tất cả 15 số hạng. A. 13 B. 10 C. 17 D. 11
Đọc tiếp
Tìm n ∈ N biết khai triển nhị thức ( a + 2 ) n + 4 , a ≠ 2 có tất cả 15 số hạng.
A. 13
B. 10
C. 17
D. 11
(
x
+
2
)
n
+
5
,
(
n
∈
ℕ
)
Khai triển nhị thức có tất cả 2019 số hạng. Tìm n. A. 2018 B. 2014 C. 2013 D. 2015
Đọc tiếp
( x + 2 ) n + 5 , ( n ∈ ℕ ) Khai triển nhị thức có tất cả 2019 số hạng. Tìm n.
A. 2018
B. 2014
C. 2013
D. 2015
Cho khai triển nhị thức Niuton
x
2
+
2
n
x
n
với n
n
∈
ℕ
, x 0. Biết rằng số hạng thứ 2 của khai triển bằng 98 và n thỏa mãn
A
n...
Đọc tiếp
Cho khai triển nhị thức Niuton x 2 + 2 n x n với n n ∈ ℕ , x > 0. Biết rằng số
hạng thứ 2 của khai triển bằng 98 và n thỏa mãn A n 2 + 6 C n 3 = 36 n Trong các giá trị x sau, giá trị nào thỏa mãn?
A. 3
B. 4
C. 1
D. 2
Khi khai triển nhị thức Newton
G
(
x
)
a
x
+
a
n
thì ta thấy trong đó xuất hiện hai số hạng 24x và 252
x
2
. Tìm a và n A. a3, n8 B. a2, n7 C. a4, n9 D. a5, n10
Đọc tiếp
Khi khai triển nhị thức Newton G ( x ) = a x + a n thì ta thấy trong đó xuất hiện hai số hạng 24x và 252 x 2 . Tìm a và n
A. a=3, n=8
B. a=2, n=7
C. a=4, n=9
D. a=5, n=10