Các câu hỏi tương tự
Trên một tờ giấy có kẻ dòng, chọn khoảng cách giữa hai dòng làm đơn vị độ dài, vẽ 5 đường tròn cùng tâm I có bán kính lần lượt bằng 1, 2, 3, 4, 5 (đơn vị độ dài). Đánh dấu các đường tròn này theo thứ tự là (1), (2), (3), (4), (5). Trên một tờ giấy kính, kẻ hệ trục tọa độ Oxy, trên tia Oy lấy điểm K sao cho OK ½ (đơn vị độ dài nói trên). Lấy điểm H(0 ; -1/2). Qua H kẻ đường thẳng Ht // Ox.- Đặt tờ giấy kính lên tờ giấy đã vẽ 5 đường tròn sao cho đường tròn (1) đi qua K và tiếp xúc với Ht và tâm...
Đọc tiếp
Trên một tờ giấy có kẻ dòng, chọn khoảng cách giữa hai dòng làm đơn vị độ dài, vẽ 5 đường tròn cùng tâm I có bán kính lần lượt bằng 1, 2, 3, 4, 5 (đơn vị độ dài). Đánh dấu các đường tròn này theo thứ tự là (1), (2), (3), (4), (5). Trên một tờ giấy kính, kẻ hệ trục tọa độ Oxy, trên tia Oy lấy điểm K sao cho OK = ½ (đơn vị độ dài nói trên). Lấy điểm H(0 ; -1/2). Qua H kẻ đường thẳng Ht // Ox.
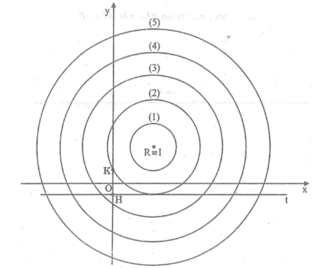
- Đặt tờ giấy kính lên tờ giấy đã vẽ 5 đường tròn sao cho đường tròn (1) đi qua K và tiếp xúc với Ht và tâm I nằm bên phải Oy. Trên tờ giấy kính, đánh dấu vào chỗ điểm I xuất hiện và kí hiệu là điểm A.
- Di chuyển tờ giấy kính sang trái sao cho đường tròn (2) đi qua K và tiếp xúc với Ht. Trên tờ giấy kính, đánh dấu vào chỗ điểm I xuất hiện và kí hiệu là điểm B (xem hình dưới).
- Tiếp tục làm như thế đối với các đường tròn còn lại ta lần lượt được các điểm C, D, E trên tờ giấy kính.
- Lấy các điểm A’, B’, C’, D’, E’ lần lượt đối xứng với các điểm A, B, C, D, E qua Oy.
- Nối các điểm E’, D’, C’, B’, A’, A, B, C, D, E bởi một đường cong ta được một parabol.
Cho nửa đường tròn tâm O đường kính BC và một điểm A trên nửa đường tròn đó ( cung AB > AC ) . Các tiếp tuyến với đường trong O tại A và B cắt nhau tại D. Gọi E là giao điểm của tia CA và tia BD; F là giao điểm của tia BD và tia AO; K là giao điểm của tia DA và tia BC. Cmr: Tia FC vuông góc với tia EK
Cho Delta ABC có góc A 90. vẽ đường tròn (O) đường kính AB và đường tròn (O) duog kính AC, Đường thẳng AB cắt đường tròn (O) tại điểm thứ 2 là D, đường thẳng AC cắt đường tròn (O) tại điểm thứ 2 là E.a) c/m 4 điểm B,C,D,E cũng nằm trên 1 đường trònb) Gọi F là giao điểm của 2 đường tròn O) và (O)(F khác A). c/m 3 điểm B,F,C thẳng hàng và FA là tia phân giacgoc EFDc) goi H la giao diem cua ab va Ef, c,m A la tam duong tron noi diep Delta DEF va BH.AD AH.BDGIÚP MK CÂU b với CÂU c ĐI, TKS truoc
Đọc tiếp
Cho \(\Delta ABC\) có góc A > 90. vẽ đường tròn (O) đường kính AB và đường tròn (O') duog kính AC, Đường thẳng AB cắt đường tròn (O') tại điểm thứ 2 là D, đường thẳng AC cắt đường tròn (O) tại điểm thứ 2 là E.
a) c/m 4 điểm B,C,D,E cũng nằm trên 1 đường tròn
b) Gọi F là giao điểm của 2 đường tròn O) và (O')(F khác A). c/m 3 điểm B,F,C thẳng hàng và FA là tia phân giacgoc EFD
c) goi H la giao diem cua ab va Ef, c,m A la tam duong tron noi diep \(\Delta DEF\) va BH.AD= AH.BD
GIÚP MK CÂU b với CÂU c ĐI, TKS truoc
Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc đường tròn (O), với C khác A và B, biết CA CB. Lấy điểm M thuộc đoạn OB, với M khác O và B. Đường thẳng đi qua điểm M vuông góc với AB cắt hai đường thẳng AC và BC lần lượt tại hai điểm D và H.1) Chứng minh bốn điểm A, C, H, M cùng thuộc một đường tròn và xác định tâm của đường tròn này.2) Chứng minh: MA.MB MD.MH3) Gọi E là giao điểm của đường thẳng BD với đường tròn (O), E khác B. Chứng minh ba điểm A, H, E thẳng hàng.4) Trên tia đối của tia...
Đọc tiếp
Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc đường tròn (O), với C khác A và B, biết CA < CB. Lấy điểm M thuộc đoạn OB, với M khác O và B. Đường thẳng đi qua điểm M vuông góc với AB cắt hai đường thẳng AC và BC lần lượt tại hai điểm D và H.
1) Chứng minh bốn điểm A, C, H, M cùng thuộc một đường tròn và xác định tâm của đường tròn này.
2) Chứng minh: MA.MB = MD.MH
3) Gọi E là giao điểm của đường thẳng BD với đường tròn (O), E khác B. Chứng minh ba điểm A, H, E thẳng hàng.
4) Trên tia đối của tia BA lấy điểm N sao cho MN = AB, Gọi P và Q tương ứng là hình chiếu vuông góc của điểm M trên BD và N trên AD.
Chứng minh bốn điểm D, Q, H, P cùng thuộc một đường tròn.
Bài 6: Cho đường tròn (O; R) và dây AB, gọi I là trung điểm của dây AB. Trên tia dối của tia BA lấy điểm M. Kẻ hai tiếp tuyến MC, MD với đường tròn, (C,D ≠ (O)) .
a) Chứng minh rằng: Năm điểm O, I, C, M, D cùng nằm trên một đường tròn.
b) Gọi N là giao điểm của tia OM với (O). Chứng minh rằng N là tâm đường tròn nội tiếp .
Bài 5. Cho đường tròn (O) và một điểm M nằm bên ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB (A và B là tiếp điểm) và cát tuyến MNP (N nằm giữa M và P) với đường tròn . Gọi E là trung điểm của NP a) Chứng minh rằng năm điểm M, A, K, O, B cùng nằm trên một đường tròn, từ đó chứng minh KM là tia phân giác của AKB b) Gọi Q là giao điểm thứ hai của đường thẳng BK với đường tròn (O).Chứng minh AQ//NP c) Gọi H là giao điểm của AB và MO. Chứng minh rằng: MH.MO MB2 ; MH.MO MN.MP d) Chứng minh tứ giác...
Đọc tiếp
Bài 5. Cho đường tròn (O) và một điểm M nằm bên ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB (A và B là tiếp điểm) và cát tuyến MNP (N nằm giữa M và P) với đường tròn . Gọi E là trung điểm của NP a) Chứng minh rằng năm điểm M, A, K, O, B cùng nằm trên một đường tròn, từ đó chứng minh KM là tia phân giác của AKB b) Gọi Q là giao điểm thứ hai của đường thẳng BK với đường tròn (O).Chứng minh AQ//NP c) Gọi H là giao điểm của AB và MO. Chứng minh rằng: MH.MO= MB2 ; MH.MO= MN.MP d) Chứng minh tứ giác NHOP nội tiếp e) Gọi E là giao điểm của AB và KO, F là giao điểm của AB và NP. CMR: AB2=4 HE.HF và tứ giác KEMH nội tiếp f) Chứng minh: EN, EP là các tiếp tuyến của (O)
Gọi C và D là hai điểm trên nửa đường tròn tâm O đường kính AB=2R sao cho C thuộc cung AD và góc COD bằng 90 độ. E là giao điểm của hai dây AD và BC, F là giao điểm của các đường thẳng AC và BD
a) Chứng minh bốn điểm C, E, D, F cùng nằm trên một đường tròn
b) Gọi I là trung điểm của EF. Chứng minh ID là tiếp tuyến của đường tròn (O)
CÁC BẠN LÀM LUÔN GIÚP MÌNH VỚI !
Gọi C và D là hai điểm trên nửa đường tròn tâm O đường kính AB=2R sao cho C thuộc cung AD và góc COD bằng 90 độ. E là giao điểm của hai dây AD và BC, F là giao điểm của các đường thẳng AC và BD
a) Chứng minh bốn điểm C, E, D, F cùng nằm trên một đường tròn
b) Gọi I là trung điểm của EF. Chứng minh ID là tiếp tuyến của đường tròn (O)
CÁC BẠN LÀM LUÔN GIÚP MÌNH VỚI !
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng