6 tháng 6 2022 lúc 14:56
Bài 2: Cực trị hàm số
Các câu hỏi tương tự
Cho hàm số \(y=x^4-2m\left(m+1\right)x^2+m^2\) với m là tham số thực.
a) Tìm m để đồ thị hàm số trên có 3 cực trị tạo thành 3 đỉnh của tâm giác vuông
b) Tìm m để đồ thị hàm số trên có 3 cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
Mọi người giúp mình với ạ!!! Mình cảm ơn rất nhiều!!!
1, Viết phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số:
\(y=x^3-6x^2-3x+2\)
2, Cho hàm số: \(y=x^3-x^2+mx\)
Tìm m để đồ thị hàm số có các điểm cực đại, cực tiểu: A, B sao cho Δ OAB vuông góc tại O.
với m bằng bao nhiêu thì đồ thị hàm số y = x³ + 2mx² - m có 2 điểm cực trị đồng thời hai điểm cực trị này tạo với gốc tọa độ O một tam giác vuông tại O
Xem chi tiết
Tìm m để đồ thị hàm số y = x4 - m.x2 + 4.x + m có 3 điểm cực trị A , B , C sao cho gốc tọa độ là trọng tâm tam giác ABC.
Các bạn giúp mình bài tập này với !
Bài 1: Cho hàm số yx^3+3x^2+mx+m-2 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoànhBài 2: Cho hàm số ydfrac{2x-2}{x+1} . Tìm m để đường thẳng d: y2x+m cắt đồ thị (C) tại 2 điểm phân biệt A, B sao cho ABsqrt{5}Bài 3: Cho hàm số ydfrac{1}{3}x^3-mx^2+2(m-1)x-3 (m là tham số) có đồ thị là (Cm) . Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về cùng một phía đối với trục tungBài 4: Cho hàm số y-x^3+2(m-1)x^2-(m^2-3m+2)x-...
Đọc tiếp
Bài 1: Cho hàm số \(y=x^3+3x^2+mx+m-2\) (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành
Bài 2: Cho hàm số \(y=\dfrac{2x-2}{x+1}\) . Tìm m để đường thẳng d: \(y=2x+m\) cắt đồ thị (C) tại 2 điểm phân biệt A, B sao cho AB=\(\sqrt{5}\)
Bài 3: Cho hàm số \(y=\dfrac{1}{3}x^3-mx^2+2(m-1)x-3\) (m là tham số) có đồ thị là (Cm) . Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về cùng một phía đối với trục tung
Bài 4: Cho hàm số \(y=-x^3+2(m-1)x^2-(m^2-3m+2)x-4\)
(m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung
Bài 5: Cho hàm số \(y=-x^3+3x^2+3(m^2-1)x-3m^2-1\) (1). Tìm m để hàm số (1) có cực đại, cực tiểu, đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác vuông tại O
Tìm tất cả các giá trị thực của tham số m để hàm số y = x^3 - (3m +1).x^2 + (2m -1)x +m +1 . Có bao nhiêu số tự nhiên m<100 để đồ thị hs có hai điểm cực trị nằm về 2 phía của trục hoành.
Cho hàm số : \(y=f\left(x\right)=x^4+2\left(m-2\right)x^2+m^2-5m+5\)
Tìm các giá trị của m để đồ thị hàm số có các điểm cực đại và cực tiểu tạo thành 1 tam giác vuông cân
Cho hàm số : \(y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\left(1\right)\)
Tìm m để hàm số (1) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến góc tọa độ O bằng \(\sqrt{2}\) lần khoảng cách từ cực tiểu của đồ thị hàm số đến góc tọa độ O
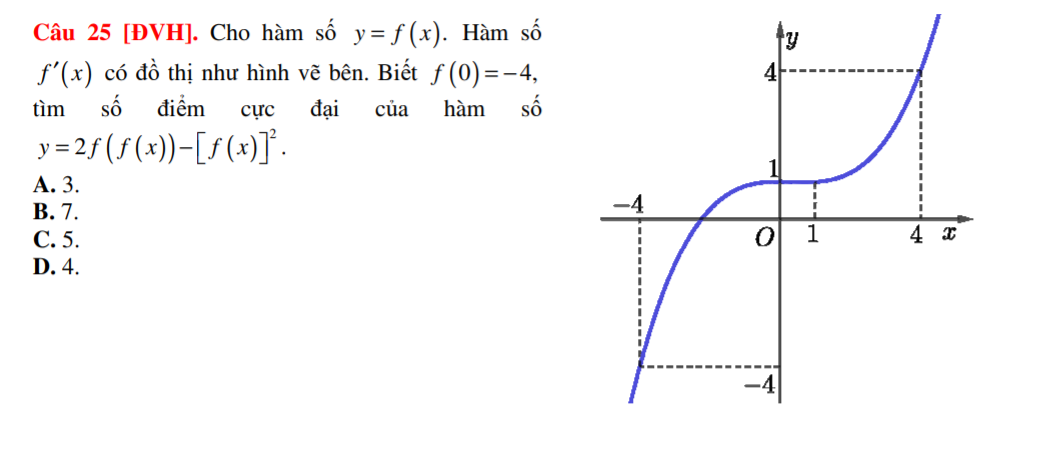
Cho hàm số \(y=\frac{1}{4}x^4-\left(3m+1\right)x^2+2\left(m+1\right)\), m là tham số . Tìm m để đồ thị hàm số đã cho có 3 điểm cực trị lập thành 1 tam giác có trọng tâm là gốc tọa độ
Cho hàm số y=f(x). Hàm số f'(x) có đồ thị như hĩnh vẽ bên:. Biết f(0) = -4, tìm số điể cực đại của hàm số y= 2.f (f(x)) - [ f(x)]2