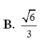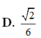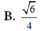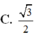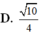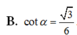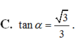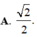Trong các mệnh đề sau đây, mệnh đề nào là sai?
A. Cho a, b là hai đường thẳng chéo nhau và vuông góc với nhau. Đường vuông góc chung của a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia
B. Không thể có một hình chóp tứ giác S.ABCD nào có hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy
C. Cho u → , n → là hai véctơ chỉ phương của hai đường thẳng cắt nhau nằm trong mặt phẳng ( α ) và n → là véctơ chỉ phương của đường thẳng ∆ . Điều kiện cần và đủ để ∆ ⊥ ( α ) là u → . n → = 0 v à n → . v → = 0
D. Hai đường thẳng a và b trong không gian có các véctơ chỉ phương lần lượt là u → , n → . Điều kiện cần và đủ để a và b chéo nhau là a và b không có điểm chung và hai véctơ u → , n → không cùng phương
D. Hai đường thẳng a và b trong không gian có các véctơ chỉ phương lần lượt là a → v à b → . Điều kiện cần và đủ để a và b chéo nhau là a và b không có điểm chung và hai véctơ a → v à b → không cùng phương
Đáp án B
Tồn tại một hình chóp tứ giác S.ABCD có hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy