Hình gồm một đường tròn và một tam giác đều nội tiếp không có tâm đối xứng.
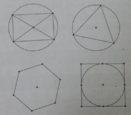
Đáp án B
Hình gồm một đường tròn và một tam giác đều nội tiếp không có tâm đối xứng.

Đáp án B
Tính diện tích lớn nhất S m a x của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R = 6 cm nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp

A. S m a x = 36 πcm 2
B. S m a x = 36 c m 2
C. S m a x = 96 πcm 2
D. S m a x = 18 c m 2
Cho tam giác ABC nội tiếp đường tròn (O). Qua O kẻ đường thẳng d. Quy tắc nào sau đây là một phép biến hình:

A. Quy tắc biến O thành giao điểm của d với các cạnh tam giác ABC
B. Quy tắc biến O thành giao điểm của d với đường tròn (O)
C. Quy tắc biến O thành hình chiếu của O trên các cạnh của tam giác ABC
D. Quy tắc biến O thành trực tâm H, biến H thành O và các điểm khác H và O thành chính nó
Cho đa giác đều 20 đỉnh nội tiếp trong đường tròn tâm O. Chọn ngẫu nhiên 4 đỉnh của đa giác. Xác suất để 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật bằng
A. 7 216
B. 9 969
C. 3 323
D. 4 9
Cho đa giác đều 20 đỉnh nội tiếp đường tròn tâm O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất được chọn là 4 đỉnh của một hình chữ nhật?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 0 . Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
A . V T V N = 2 6
B . V T V N = 2 3
C . V T V N = 3 2
D. Đáp án khác
Cho tứ diện đều ABCD có cạnh bằng 4. Tính diện tích xung quanh S x q của hình trụ có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD.
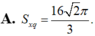
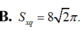
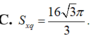
![]()
Cho tứ diện đều ABCD có cạnh bằng 4. Tính diện tích xung quanh S x q của hình trụ có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD.
![]()
![]()
![]()
![]()
Cho chóp tứ giác S.ABCD có đáy là hình vuông cạnh 2a và tam giác SAD đều đồng thời nằm trong mặt phẳng vuông góc đáy. Tính khoảng cách d từ tâm đường tròn nội tiếp tam giác SAD đến mặt phẳng (SBC) theo a
A. d = 2 a 21 7
B. d = 4 a 57 57
C. d = 2 a 21 21
D. d = 4 a 21 21
Cho đa giác đều 20 đỉnh nội tiếp đường tròn tâm O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật.
![]()
B. 1728 28561
![]()
![]()
Cho một đa giác đều 20 đỉnh nội tiếp trong đường tròn O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật
A. 3 323
B. 4 9
C. 2 969
D. 7 216