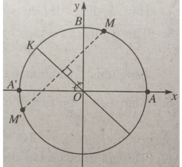
Sđ MK = sđ KM’ = 55 o
⇒ sđ AM’ = sđ AM + sđ MK + sđ KM’ = 190 o .
Đáp án: C

Sđ MK = sđ KM’ = 55 o
⇒ sđ AM’ = sđ AM + sđ MK + sđ KM’ = 190 o .
Đáp án: C
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = - 70 o với A(1; 0). Gọi M 1 là điểm đối xứng của M qua đường phân giác của góc phần tư thứ I. Số đo của cung lượng giác A M 1 là
A . - 150 ο B . 220 ο C . 160 ο D . - 160 ο
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM = α (0 < α < π/2). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo các cung AM1, AM2, AM3.
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Cho tam giác nhọn ABC nội tiếp đường tròn (O) với AB<AC .Đường phân giác của góc B A C ^ cắt (O) tại điểm D khác A
Gọi M là trung điểm của AD và E là điểm đối xứng với D qua tâm O.
Giả sử đường tròn ngoại tiếp tam giác ABM cắt đoạn thẳng AC tại điểm F khácA
2). Chứng minh rằng È vuông góc với AC
Cho tam giác nhọn ABC nội tiếp đường tròn (O) với AB<AC. Đường phân giác của góc B A C ^ cắt (O) tại điểm D khác A
Gọi M là trung điểm của AD và E là điểm đối xứng với D qua tâm O.
Giả sử đường tròn ngoại tiếp tam giác ABM cắt đoạn thẳng AC tại điểm F khácA
1) Chứng minh rằng tam giác ĐM và tam giác BCF đồng dạng.
Trên đường tròn lượng giác gốc A, xác định các điểm M khác nhau biết rằng cung AM có số đo tương ứng là (trong đó k là một số nguyên tùy ý)