Ta có: 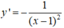
- Lấy điểm M(x0;y0) ∈ (C).
- Phương trình tiếp tuyến tại điểm M là:
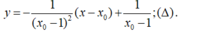
+ Giao với trục hoành: 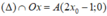
+ Giao với trục tung: 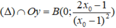
- Ta có:
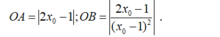
- Theo giả thiết tam giác OAB có diện tích bằng 2 nên:
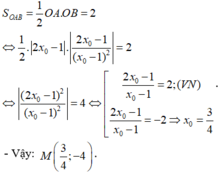
Ta có: 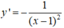
- Lấy điểm M(x0;y0) ∈ (C).
- Phương trình tiếp tuyến tại điểm M là:
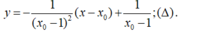
+ Giao với trục hoành: 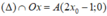
+ Giao với trục tung: 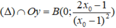
- Ta có:
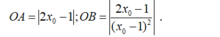
- Theo giả thiết tam giác OAB có diện tích bằng 2 nên:
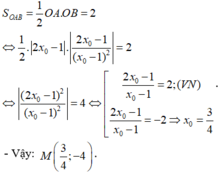
Trên đồ thị của hàm số y = 1 x - 1 có điểm M sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo thành một tam giác có diện tích bằng 2. Tọa độ M là:
A. (2;1)
B. 4 ; 1 3
C. - 3 4 ; - 4 7
D. 3 4 ; - 4
Cho hàm số y = 2 x + m + 1 x - 1 C m . Tìm m để tiếp tuyến của C m tại điểm có hoành độ x 0 = 2 tạo với hai trục tọa độ một tam giác có diện tích bằng 25 2 .
A. m = - 2 ; m = - 23 9 m = - 7 ; m = - 28 9
B. m = 2 ; m = 23 9 m = - 7 ; m = - 28 9
C. m = - 2 ; m = - 23 9 m = 7 ; m = 28 9
D. m = 2 ; m = - 23 9 m = 7 ; m = - 28 9
Cho hàm số y = 2 x + m + 1 x - 1 C m . Tìm m để tiếp tuyến của C m tại điểm có hoành độ x 0 = 2 tạo với hai trục tọa độ một tam giác có diện tích bằng 25/2.
A. m = - 2 ; m = - 23 9 m = - 7 ; m = - 28 9
B. m = 2 ; m = 23 9 m = - 7 ; m = - 28 9
C. m = - 2 ; m = - 23 9 m = 7 ; m = 28 9
D. m = 2 ; m = - 23 9 m = 7 ; m = - 28 9
Cho hàm số y = 3 x + 1 x + 1 1 . Diện tích của tam giác tạo bởi các trục tọa độ và tiếp tuyến của đồ thị của hàm số (1) tại điểm M(-2; 5) là a/b ( phân số tối giản) .Tính a + b.
A: 81
B: 4
C: 85
D: đáp án khác
Cho hàm số: y = 2 x + 2 x - 1 có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến tạo với 2 trục tọa độ lập thành một tam giác cân.
A. y = -x-1; y = -x+6
B. y = -x-2; y = -x+7
C. y = -x-1; y = -x+5
D. y = -x-1; y = -x+7
Có mấy điểm M ∈ C : y = x - 1 2 x + 2 sao cho tiếp tuyến với (C) tại M tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên đường thẳng d: 4x + y = 0 ?Có mấy điểm sao cho tiếp tuyến với (C) tại M tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên đường thẳng d: 4x + y = 0 ?
A: không có
B: 1
C: 2
D: 3
Cho hàm số y = 2 x x + 1 C . Có mấy điểm M ∈ (C), biết tiếp tuyến của (C) tại M cắt hai trục tọa độ tại A; B và tam giác OAB có diện tích bằng 1/4.
A: 0
B: 1
C: 2
D: 3
Cho hàm số y = x + 2 2 x + 3 1 . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0.
A: x + y = 0
B: x + y + 2 = 0
C: x + y – 2 = 0
D: Cả A và C đúng
Tiếp tuyến của parabol y = 4 - x 2 tại điểm (1; 3) tạo với hai trục tọa độ một tam giác vuông. Diện tích của tam giác vuông đó là:
A. 25 2
B. 5 4
C. 5 2
D. 25 4