Các câu hỏi tương tự
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau? 1. Phương trình vô nghiệm trên trường số thực R. 2. Phương trình vô nghiệm trên trường số phức C 3. Phương trình không có nghiệm thuộc tập số thực. 4. Phương trình có bốn nghiệm thuộc tập số phức. 5. Phương trình chỉ có hai nghiệm là số phức. 6. Phương trình có hai nghiệm là số thực A. 0. B. 1. C. 3. D. 2.
Đọc tiếp
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Số phức za+bi, a,b thuộc R là nghiệm của phương trình
(
z
-
1
)
(
1
+
i
z
z
-
1
z
i
. Tổng Ta^2+b^2 bằng A. . B. . C. D. .
Đọc tiếp
Số phức z=a+bi, a,b thuộc R là nghiệm của phương trình ( z - 1 ) ( 1 + i z z - 1 z = i . Tổng T=a^2+b^2 bằng
A. ![]() .
.
B. ![]() .
.
C.![]()
D. ![]() .
.
Giá trị của các số thực b, c để phương trình
z
2
+
b
z
+
c
0
nhận số phức
z
1
+
i
làm một nghiệm là: A.
b
2
c...
Đọc tiếp
Giá trị của các số thực b, c để phương trình z 2 + b z + c = 0 nhận số phức z = 1 + i làm một nghiệm là:
A. b = 2 c = - 2
B. b = - 2 c = - 2
C. b = - 2 c = 2
D. b = 2 c = 2
Giá trị của các số thực b ; c để phương trình z2 + bz + c 0 nhận số phức z 1 + i làm một nghiệm là: A. B. C. D.
Đọc tiếp
Giá trị của các số thực b ; c để phương trình z2 + bz + c = 0 nhận số phức z =1 + i làm một nghiệm là:
A. 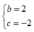
B. 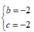
C. 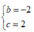
D. 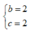
Số phức z nào dưới đây là nghiệm của phương trình:
(
-
1
+
i
)
z
4
-
3
(
2
-
i
)
z
2
+
(
16
i
+
2
)
0
A. z i B. z -i C. z i + 1 D. z 5
Đọc tiếp
Số phức z nào dưới đây là nghiệm của phương trình: ( - 1 + i ) z 4 - 3 ( 2 - i ) z 2 + ( 16 i + 2 ) = 0
A. z = i
B. z = -i
C. z = i + 1
D. z = 5
Phương trình z 2 + a z + b = 0 có một nghiệm phức là z = 1 + 2 i . Tổng 2 số a và b bằng:
A. 0
B. -3
C. 3
D. -4
Phương trình
z
2
+
a
z
+
b
0
có một nghiệm phức là
z
1
+
2
i
.
Tổng 2 số a và b bằng: A. 0 B. -3 C. 3 D. -4
Đọc tiếp
Phương trình z 2 + a z + b = 0 có một nghiệm phức là z = 1 + 2 i . Tổng 2 số a và b bằng:
A. 0
B. -3
C. 3
D. -4
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
A. -1
B. -2
C. -3
D. -4
Gọi z1; z2 là hai nghiệm phức của phương trình z2 – z + 1 0 . Tìm phần thực, phần ảo của số phức lần lượt là? A. 0; 1 B. 1; 0 C. -1; 0 D. 0; -1
Đọc tiếp
Gọi z1; z2 là hai nghiệm phức của phương trình z2 – z + 1 = 0 . Tìm phần thực, phần ảo của số phức ![]() lần lượt là?
lần lượt là?
A. 0; 1
B. 1; 0
C. -1; 0
D. 0; -1




