Các câu hỏi tương tự
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ A(1;2;1), C(3;6;-3). Gọi M là một điểm bất kỳ thuộc mặt cầu
(
S
)
:
x
-
2
2
+
y
-
4
2...
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ A(1;2;1), C(3;6;-3). Gọi M là một điểm bất kỳ thuộc mặt cầu ( S ) : x - 2 2 + y - 4 2 + z + 1 2 = 1 . Tính tổng các khoảng cách từ điểm M đến tất cả các mặt của hình lập phương ABCD.A'B'C'D'.
A. 2 3
B. 3 3
C. 6 3
D. 12
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ các đỉnh A(0;0;0), B(1;0;0), C(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADDA Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0), B(1;0;0), C(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A' Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
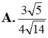
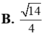
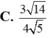
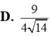
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi
S
1
là diện tích 6 mặt của hình lập phương,
S
2
là diện tích xung quanh của hình trụ. Tỉ số
S
2
/
S
1
bằng:A.
π...
Đọc tiếp
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Lập phương trình của mặt phẳng (α) đi qua điểm M(1; 2; 3) và cắt ba tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất.
Cho khối lập phương ABCD.ABCD cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MBDN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:A.
a
3
9
B.
a
3
6
C.
a...
Đọc tiếp
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Biết rằng thể tích của một khối lập phương bằng 8. Tính tổng diện tích các mặt của hình lập phương đó. A. 16 B. 24 C. 36 D. 27.
Đọc tiếp
Biết rằng thể tích của một khối lập phương bằng 8. Tính tổng diện tích các mặt của hình lập phương đó.
A. 16
B. 24
C. 36
D. 27.
Tổng diện tích các mặt của một hình lập phương bằng 54. Thể tích của khối lập phương là:
A. 15.
B. 27.
C. 18.
D. 21.
Một khối rubik có hình lập phương (mỗi mặt của rubik có 9 ô vuông) có thể tích bằng 125
c
m
3
. Hỏi tổng diện tích các mặt của khối rubik đó bằng bao nhiêu? A.
150
c
m
2
B.
25
c
m
2
C.
54
c
m
2
D. ...
Đọc tiếp
Một khối rubik có hình lập phương (mỗi mặt của rubik có 9 ô vuông) có thể tích bằng 125 c m 3 . Hỏi tổng diện tích các mặt của khối rubik đó bằng bao nhiêu?
A. 150 c m 2
B. 25 c m 2
C. 54 c m 2
D. 108 c m 2
Diện tích một mặt của hình lập phương là 9. Thể tích khối lập phương đó là:
A. 729.
B. 81.
C. 27.
D. 9.




