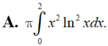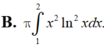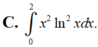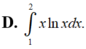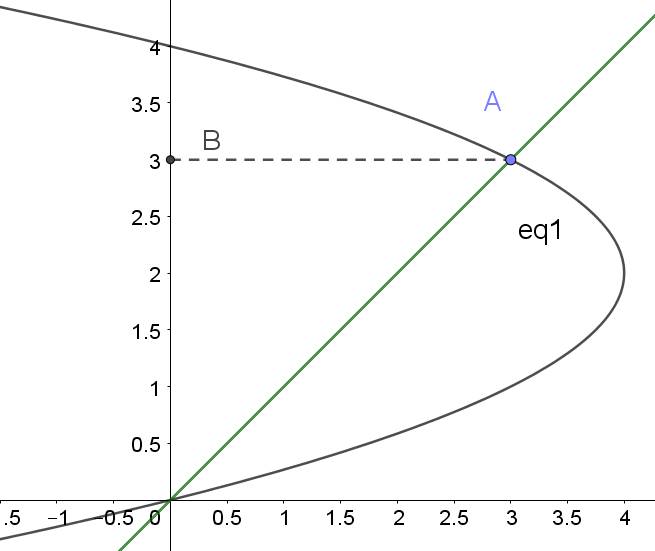
Hình minh hoạ.
Xét phương trình tung độ giao điểm
$y=4y-y^2$
\(\Leftrightarrow y=3\) hoặc \(y=0\).
Thể tích cần tìm là \(\int_0^3\pi\left|y^2-\left(4y-y^2\right)^2\right|dy=66\pi\).

Hình minh hoạ.
Xét phương trình tung độ giao điểm
$y=4y-y^2$
\(\Leftrightarrow y=3\) hoặc \(y=0\).
Thể tích cần tìm là \(\int_0^3\pi\left|y^2-\left(4y-y^2\right)^2\right|dy=66\pi\).
Tính thể tích V của vật thể tròn xoay sinh ra bởi hình phẳng giới hạn bởi đường cong y = x , trục tung và đường thẳng y=2 quay quanh trục Oy.
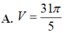
![]()
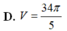
Thể tích vật thể tròn xoay được giới hạn bởi các đường y = 1 - x 2 , y = 0 , x = 0 khi quay quanh trục Oy là:
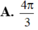
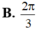
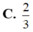
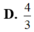
Cho hình phẳng (D) giới hạn bởi các đường y = ( x - 2 ) 2 và y = 4 . Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Oy
A. 219 π 2
B. 172 π 5
C. 113 π 2
D. 128 π 3
Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 0 ; y = x ; y = x - 2
A. 8 π 3
B. 16 π 3
C. 10 π
D. 8 π
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng y = ln x ; y = 0 ; x = 1 ; x = e
A. e - 2
B. e + 2
C. π ( e + 2 )
D. π ( e - 2 )
Gọi D là miền giới hạn bởi (P): y = 2x - x2 và trục hoành. Tính thể tích vật thể V do ta quay (D) xung quanh trục Oy.
A. 12 π 13
B. 8 π 3
C. 2 π 9
D. π 15
Tính thể tích V của vật thể sinh ra bởi phép quay quanh trục Ox của hình (H) giới hạn bởi các đường y = log 2 x , x+y-3=0; y=0
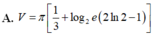

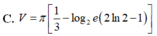
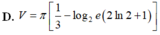
Cho tam giác giới hạn bởi ba đường y = x, x = 1 và trục Ox. Tính thể tích khối tròn xoay được tạo bởi phép quay tam giác đó quanh trục Oy.
A. π 3
B. 2 π 3
C. π
D. 4 π 3
Tính thể tích V của khối tròn xay nhận được khi quay quanh trục Oy hình phẳng giới hạn bởi các đường x = 2 y y 2 + 1 , y = 0, y = 1.
A. V = π 3
B. V = π 2
C. V = π 4
D. V = 3 π 2
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y = x ln x y = 0 ; x = 2 quay quanh trục Ox được tính bởi công thức nào?