Các câu hỏi tương tự
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi y = |2x – x2|, y = 0 và x = 3 , quanh :
• Trục Ox
• Trục Oy
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởia) , x 0 và tiếp tuyến với đường tại điểm có hoành độ x 1, quanh trục Oy;b) , y 0, y 2x, quanh trục Oxc) y |2x – x2|, y 0 và x 3 , quanh :• Trục Ox• Trục Oy
Đọc tiếp
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi
a) 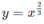 , x = 0 và tiếp tuyến với đường
, x = 0 và tiếp tuyến với đường 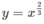 tại điểm có hoành độ x = 1, quanh trục Oy;
tại điểm có hoành độ x = 1, quanh trục Oy;
b) 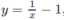 , y = 0, y = 2x, quanh trục Ox
, y = 0, y = 2x, quanh trục Ox
c) y = |2x – x2|, y = 0 và x = 3 , quanh :
• Trục Ox
• Trục Oy
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi:
a) y = 2 – x 2 , y = 1 , quanh trục Ox.
b) y = 2x – x 2 , y = x , quanh trục Ox.
c) 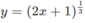 ,x = 0, y = 3, quanh trục Oy.
,x = 0, y = 3, quanh trục Oy.
Gọi (D) là hình phẳng giới hạn bởi các đường
y
2
x
,
y
0
,
x
0
v
à
x
2
. Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức: A.
V
π
∫
0
2...
Đọc tiếp
Gọi (D) là hình phẳng giới hạn bởi các đường y = 2 x , y = 0 , x = 0 v à x = 2 . Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức:
A. V = π ∫ 0 2 2 x + 1 d x
B. V = ∫ 0 2 2 x + 1 d x
C. V = ∫ 0 2 4 x d x
D. V = π ∫ 0 2 4 x d x
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi: y = 2x – x 2 , y = x , quanh trục Ox.
Cho hình phẳng (D) được giới hạn bởi các đường x0, x1, y0 và
y
2
x
+
1
.Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0, x=1, y=0 và y = 2 x + 1 .Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
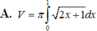
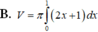
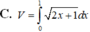
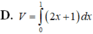
Cho hình phẳng (D) được giới hạn bởi các đường x 0; x 1; y 0 và
y
2
x
+
1
. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x = 0; x = 1; y = 0 và y = 2 x + 1 . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
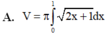
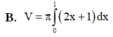
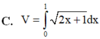
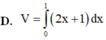
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi: y = 2 – x 2 , y = 1 , quanh trục Ox.
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường y
1
x
, y 0, x 1 và x a (a 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → +
∞
(tức là
lim
a
→
+
∞
V...
Đọc tiếp
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường y = 1 x , y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → + ∞ (tức là lim a → + ∞ V a ).



