Các câu hỏi tương tự
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 1/sinx trên đoạn [ π /3; 5 π /6]
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Cho hình lập phương ABCD.ABCD. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó:
V
H
V
ABCD
.
A
B
C
D...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó: V H V ABCD . A ' B ' C ' D '
A. 1/3 B. π /6
C. π /8 D. π /12
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
1
1
+
sin
2
x
với
x
∈
R
{
-
π
4
+
k
π
,
k
∈
}...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 1 + sin 2 x với x ∈ R { - π 4 + k π , k ∈ } . Biết F(0)=1,F( π )=0, tính giá trị biểu thức P = F ( - π 12 ) - F ( 11 π 12 )
![]()
![]()
![]()
![]()
Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π/2) là:
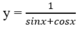
A. 1 B. 2 2
C. - 2 D. 2/ 2
Giá trị nhỏ nhất của hàm số sau trên khoảng (0;
π
/2) là:
y
1
sinx
+
cosx
A. 1 B. 2
2
C. -
2
D.
2
/2
Đọc tiếp
Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π /2) là:
y = 1 sinx + cosx
A. 1 B. 2 2
C. - 2 D. 2 /2
Quay hình phẳng G giới hạn bởi các đường: y = x 3 ; y = 1, x = 0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:
A. π B. 5 π /3
C. 3 π /5 D. 3/5
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi
S
1
là diện tích 6 mặt của hình lập phương,
S
2
là diện tích xung quanh của hình trụ. Tỉ số
S
2
/
S
1
bằng:A.
π...
Đọc tiếp
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Quay hình phẳng Q giới hạn bởi các đường:
y
1
sinx và
y
2
2x/
π
quanh trục Ox, ta được một khối tròn xoay. Khi đó, thể tích khối tròn xoay này bằng:A. 1/6 B.
π
/6C. 8 D.
π
2
/6
Đọc tiếp
Quay hình phẳng Q giới hạn bởi các đường: y 1 = sinx và y 2 = 2x/ π quanh trục Ox, ta được một khối tròn xoay. Khi đó, thể tích khối tròn xoay này bằng:
A. 1/6 B. π /6
C. 8 D. π 2 /6
Quay hình phẳng Q giới hạn bởi các đường: y 1 = sinx và y 2 = 2x/π quanh trục Ox, ta được một khối tròn xoay. Khi đó, thể tích khối tròn xoay này bằng:
A. 1/6 B. π/6
C. 8 D. π 2 /6