Chọn D.
(Đồ thị giao với trục hoành tại điểm - 1 2 ; 0 trục tung : x = 0.
Diện tích hình cần tìm là
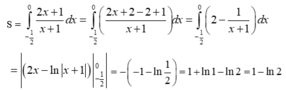
Chọn D.
(Đồ thị giao với trục hoành tại điểm - 1 2 ; 0 trục tung : x = 0.
Diện tích hình cần tìm là
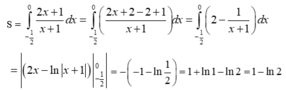
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x , trục tung, trục hoành và đường thẳng x=1 là:
A. 1
B. 2
C. 1 2
D. 3 2
Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị (C) của hàm số y = x 4 + x 2 , trục hoành, trục tung và đường thẳng x = 1. Biết S = a 5 + b , a , b ∈ ℚ . Tính a + b
A. a + b = - 1
B. a + b = 1 2
C. a + b = 1 3
D. a + b = 13 3
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x . e x , trục hoành, trục tung và đường thẳng x=1 thì diện tích hình (H) là:
![]()
![]()
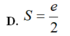
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x . e x , trục hoành, trục tung và đường thẳng x=1 thì diện tích hình (H) là
A. S = e − 1 2
B. S = 2 e − 1
C. S = 1
D. S = e 2
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 1 - 1 x 2 , trục hoành và đường thẳng x = 1 và đường thẳng x = 2.
A. 0,3
B. 0,2
C. 0,4
D. 0,5
Diện tích hình phẳng được giới hạn bởi đồ thi hàm số y = ex – e–x, trục hoành, trục tung và đường thẳng x = –1, x = 1 là:
A. 2 e + 1 e - 2
B. 2 e - 1 e - 2
C. 2 e + 1 e + 2
D. 2 e - 1 e - 1
Biết đồ thị hàm số f ( x ) = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2 .
B. S 1 S 2 = 1 4 .
C. S 1 S 2 = 1 2 .
D. S 1 S 2 = 1 .
Tính diện tích hình phẳng giới hạn bởi : Đồ thị hàm số y = e x +1 , trục hoành , đường thẳng x = 0 và đường thẳng x = 1
A.e
B. 2+e
C.e-1
D.2e+1
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = e x - e - x , trục hoành, đường thẳng x = -1 và đường thẳng x = 1.
A. e + 1 e - 2
B. 0
C. 2 e + 1 e - 2
D. e + 1 e