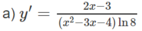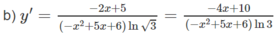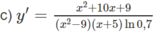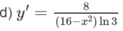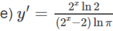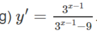Các câu hỏi tương tự
Tính đạo hàm của các hàm số cho ở bài 2.6
Cho hàm số yf(x) có đạo hàm f(x)
(
x
2
-
1
)
(
x
-
2
)
. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
f
(
x
2
+
m
)
có 5 điểm cực trị. Số phần tử của tập S là. A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số f(x) có đạo hàm
f
x
x
x
-
1
2
x
+
2
3...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' x = x x - 1 2 x + 2 3 . Số điểm cực trị của hàm số đã cho là
A. 1
B. 2
C. 3
D. 6
Cho hàm số
f
x
có đạo hàm
f
x
x
x
-
1
2
x
-
2
3
x
-
3
4
Số điểm cực trị củ...
Đọc tiếp
Cho hàm số f x có đạo hàm f ' x = x x - 1 2 x - 2 3 x - 3 4 Số điểm cực trị của hàm số đã cho là
A. 2
B. 1
C. 0
D. 3
Cho hàm số
f
x
có đạo hàm
f
x
x
x
-
1
x
+
2
3
,
∀...
Đọc tiếp
Cho hàm số f x có đạo hàm f ' x = x x - 1 x + 2 3 , ∀ x ∈ ℝ Số điểm cực trị của hàm số đã cho là
A. 3
B. 2
C. 5
D. 1
Cho hàm số f(x) có đạo hàm
f
x
x
x
-
1
x
+
2
2
,
∀
x
∈
ℝ
Số điểm cực trị của hàm số đã cho là: A. 3 B. 4 C. 2 D. 1
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' x = x x - 1 x + 2 2 , ∀ x ∈ ℝ Số điểm cực trị của hàm số đã cho là:
A. 3
B. 4
C. 2
D. 1
Cho hàm số f(x) có đạo hàm
f
x
x
+
1
x
-
2
x
+
3
2
x
-
5...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' x = x + 1 x - 2 x + 3 2 x - 5 3 . Số điểm cực trị của hàm số đã cho là
A. 4
B. 1
C. 2
D. 3
Cho hàm số f(x) có đạo hàm
f
x
x
x
-
1
x
+
2
2
∀
x
∈
ℝ
. Số điểm cực trị của hàm số đã cho là: A. 2 B. 1 C. 4 D. 3
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' x = x x - 1 x + 2 2 ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là:
A. 2
B. 1
C. 4
D. 3
Cho hàm số
y
f
x
có đạo hàm
f
x
x
2
x
-
1
x
2
-
1
3
,
∀
x
∈
ℝ
. Số điểm cực trị của hàm số đã cho l...
Đọc tiếp
Cho hàm số y = f x có đạo hàm f ' x = x 2 x - 1 x 2 - 1 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là:
A. 2
B. 1
C. 8
D. 3