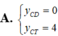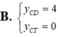Các câu hỏi tương tự
Tìm
y
C
D
(tung độ điểm cực đại) và
y
C
T
(tung độ điểm cực tiểu) của đồ thị hàm số
y
x
2
-
3
x
+
3
x
-
1
Đọc tiếp
Tìm y C D (tung độ điểm cực đại) và y C T (tung độ điểm cực tiểu) của đồ thị hàm số y = x 2 - 3 x + 3 x - 1

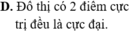
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
(
m
-
1
)
x
+
2
có cực đại, cực tiểu và các đ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
3
-
3
x
2
-
m
x
+
2
có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình:
y...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 - 3 x 2 - m x + 2 có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình: y = x - 1 ( d )
A. m = 0
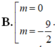
C. m = 2
D. m = - 9 2
Cho hàm số
y
x
2
-
2
m
x
+
2
x
-
m
có đồ thị (Cm), với m là tham số thực. Biết rằng hàm số đã cho có một điểm cự...
Đọc tiếp
Cho hàm số y = x 2 - 2 m x + 2 x - m có đồ thị (Cm), với m là tham số thực. Biết rằng hàm số đã cho có một điểm cực trị x 0 = 2 Tìm tung độ điểm cực tiểu của đồ thị (C).
A.![]()
B. ![]()
C. ![]()
D. ![]()
Tìm các giá trị của tham số m để đồ thị hàm số:
y
2
x
3
+
3
(
m
-
1
)
x
2
+
6
m
(
1
-...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = 2 x 3 + 3 ( m - 1 ) x 2 + 6 m ( 1 - 2 m ) x có điểm cực đại và điểm cực tiểu nằm trên đường thẳng có phương trình: y = - 4 x ( d )
A. m ∈ 1
B. m ∈ 0 ; 1
C. m ∈ 0 ; 1 2 ; 1
D. m ∈ 1 2
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
3
(
m
2
-
1
)
x
-...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Tìm hoành độ các điểm cực đại
x
C
Đ
; hoành độ các điểm cực tiểu
x
C
T
của đồ thị hàm số ysinx+cosx
Đọc tiếp
Tìm hoành độ các điểm cực đại x C Đ ; hoành độ các điểm cực tiểu x C T của đồ thị hàm số y=sinx+cosx
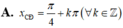
![]()
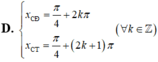
Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y (x + 1)(x – 2)2 A. 5
2
B. 2 C. 2
5
D. 4
Đọc tiếp
Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y = (x + 1)(x – 2)2
A. 5 2
B. 2
C. 2 5
D. 4
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
3
-
3
m
x
2
+
4
m
3
có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng
(...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 m x 2 + 4 m 3 có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng ( d ) : y = x .
A. m = 2 2
B. m = - 2 2
C. m = 0 h o ặ c m = 2 2 .
D. m = ± 2 2