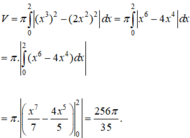
Hoành độ giao điểm hai đường cong là nghiệm của phương trình :
2 x 2 = x 3 ⇔ x 2 2 - x = 0 ⇔ x = 0 hoặc x = 2.
Vậy thể tích cần tính là :
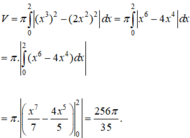
Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 0 ; y = x ; y = x - 2
A. 8 π 3
B. 16 π 3
C. 10 π
D. 8 π
Thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = tan x , x = 0 , x = π 3 và trục hoành bằng
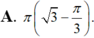
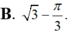
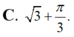
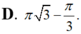
Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = x ln x , x=e và trục hoành là.
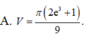
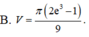
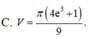
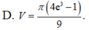
Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = x ln x , x = e và trục hoành là
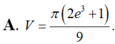
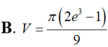
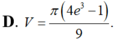
Tính thể tích V của vật tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường y = 2x2, y = x3 xung quanh trục Ox
A. V = 256 35
B. V = 256 π 35
C. V = 562 35
D. V = 562 π 35
Tính thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y=tanx; x=0; x = π 3 và trục hoành.
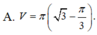
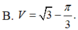
Gọi V là thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 1 x ; y = 0 ; x = 1 ; x = a , ( a > 1 ) Tìm a để V = 2.
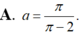
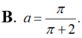
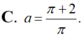
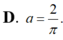
Gọi V là thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 1/x, y=0, x=1, x=a, a>1. Tìm a để V = 2.
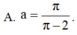
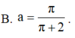
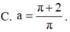
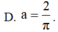
Cho hình phẳng (D) giới hạn bởi các đường y= x - 2 2 và y = 4. Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Ox
A. 118 π 5
B. 253 π 7
C. 112 π 3
D. 256 π 5
