Các câu hỏi tương tự
22 tháng 8 2021 lúc 20:21
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
22 tháng 8 2021 lúc 19:42
Câu 1: Tìm giá trị thực của tham số m để hàm số
y= \(\dfrac{1}{3}x^3-mx^{2^{ }}+\left(m^2-4\right)x+3\) tại x=3
Câu 2:Tìm m để hàm số \(y=x^3-2mx^2+mx+1\) đạt cực tiểu tại x=1
22 tháng 8 2021 lúc 20:34
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
22 tháng 8 2021 lúc 20:11
Câu 9 tìm tất cả tham số thực m để hàm số\(y=\left(m-1\right)x^4-\left(m^2-2\right)x^2+2019\) đạt cực tiểu tại x=-1
Bài 1. Cho hàm số: y 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x 1Bài 2. Cho hàm số y 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x -2 .Bài 3. Cho hàm số y 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x 2.Bài 4. Tìm tất cả tham số thực m để hàm số y (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tạix -1.Bài 5. Tìm giá trị của tham số m để hàm số y x3/3...
Đọc tiếp
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
22 tháng 8 2021 lúc 19:52
Câu 4: Tìm các giá trị thực của tham số m để hàm số\(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đạt tại x= 3
Cho hai hàm số y = (x-2)/(x-1) + (x-1)/x + x/(x+1) + (x+1)/(x-2) và y = |x-1|-x-m (với m là tham số thực). Hàm số có đồ thị lần lượt là (C1) và (C2). Tìm tập hợp m để 2 hàm số cắt nhau tại 4 điểm pb ???
Cảm ơn mn nhiều ạ
Cho hàm số yf(x) có bảng biến thiên như hình vẽ sau.Tìm tất cả các giá trị thực của tham số m để phương trình f(x) - m 0 có 4 nghiệm phân biệt. A.
m
∈
(
1
;
2
]
B.
m
∈
[
1
;
2
)
C.
m
∈
(
1
;
2
)
D.
m
∈
[...
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau.
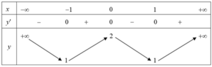
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) - m =0 có 4 nghiệm phân biệt.
A. m ∈ ( 1 ; 2 ]
B. m ∈ [ 1 ; 2 )
C. m ∈ ( 1 ; 2 )
D. m ∈ [ 1 ; 2 ]
Cho hàm số
y
f
(
x
)
liên tục trên R và có đồ thị hàm số đường cong trong hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình
|
f
(
x
)
|
m
có 4 nghiệm phân biệt. A. m ∈ (0;3) B. -3 m 1 C. Không có giá trị nào của m. D. 1 m 3
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đồ thị hàm số đường cong trong hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình | f ( x ) | = m có 4 nghiệm phân biệt.
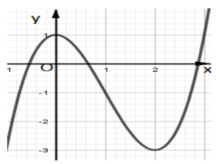
A. m ∈ (0;3)
B. -3 < m < 1
C. Không có giá trị nào của m.
D. 1 < m < 3