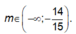Chọn A.
Ta có: ![]()
Hàm số đã cho nghịch biến trên [1;+ ∞ )khi và chỉ khi
![]()
![]()
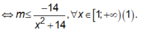
Đặt 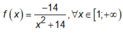
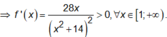
Do đó: 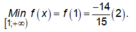
Từ (1), (2) suy ra giá trị m cần tìm là: 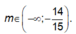
Đúng 0
Bình luận (0)
Chọn A.
Ta có: ![]()
Hàm số đã cho nghịch biến trên [1;+ ∞ )khi và chỉ khi
![]()
![]()
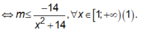
Đặt 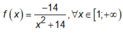
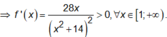
Do đó: 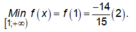
Từ (1), (2) suy ra giá trị m cần tìm là: