Các câu hỏi tương tự
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình
3
(
1
+
x
+
3
-
x
)
-
2
(
1
+
x
)
(
3
-
x
)...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 3 ( 1 + x + 3 - x ) - 2 ( 1 + x ) ( 3 - x ) ≥ m nghiệm đúng với mọi x ≤ - 1 ; 3 ?
A. m ≤ 6 .
B. m ≥ 6 .
C. m ≥ 6 2 - 4 .
D. m ≤ 6 2 - 4 .
Cho phương trình
m
.
l
n
2
(
x
+
1
)
-
(
x
+
2
-
m
)
l
n
(
x
+
1
)
-
x
-
2
0
(1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn
0...
Đọc tiếp
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2 ; 3) thuộc tập nghiệm của bất phương trình log5( x2 + 1) log5( x2 + 4x + m) - 1 (1) A. -12 ≤ m ≤ 13 B. 12 m 13 C. -12 m 12 D. Đáp án khác
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2 ; 3) thuộc tập nghiệm của bất phương trình log5( x2 + 1) > log5( x2 + 4x + m) - 1 (1)
A. -12 ≤ m ≤ 13
B. 12 < m < 13
C. -12 < m < 12
D. Đáp án khác
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm tất cả các giá trị thực của tham số m để hệ
3
2
x
+
x
+
1
-
3
2
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ 3 2 x + x + 1 - 3 2 + x + 1 + 2017 x ⩽ 2017 x 2 - ( m + 2 ) x + 2 m + 3 ⩾ 0 có nghiệm.
A. m ≤ - 2
B. m ⩾ - 3
C. m > - 3
D. m ≥ - 2
Tìm tất cả các giá trị thực của tham số m để hệ
3
2
x
+
x
+
1
-
3
2
+...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ 3 2 x + x + 1 - 3 2 + x + 1 + 2017 x ≤ 2017 x 2 - ( m + 2 ) x + 2 m + 3 ≥ 0 có nghiệm.
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình
m
.
4
x
+
(
m
-
1
)
2
x
+
2
+
m
-
1
0
nghiệm đúng
∀
x
∈
ℝ
? A.
m
≤
3
. B.
m
≥...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình m . 4 x + ( m - 1 ) 2 x + 2 + m - 1 > 0 nghiệm đúng ∀ x ∈ ℝ ?
A. m ≤ 3 .
B. m ≥ 1 .
C. - 1 ≤ m ≤ 4 .
D. m ≥ 0 .
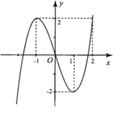
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Tìm tất cả các giá trị thực của tham số m để phương trình
64
|
x
|
3
(
x
2
+
1
)
2
(
12
|
x
|
+
m
(
x
2
+
1
)
)...
Đọc tiếp
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
A.![]()
B. Với mọi m
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để phương trình
log
2
5
x
-
1
.
log
4
2
.
5
x
-
2
m
có nghiệm x ≥ 1 A. m ∈ (-∞;2) B. m ∈ (2;+∞) C. m ∈ (3;+∞) D. m ∈ (-∞;3)
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥ 1
A. m ∈ (-∞;2)
B. m ∈ (2;+∞)
C. m ∈ (3;+∞)
D. m ∈ (-∞;3)