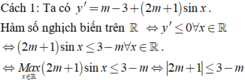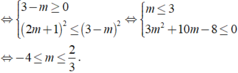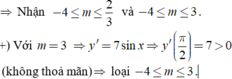Các câu hỏi tương tự
Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên
ℝ
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số ![]() nghịch biến trên
ℝ
nghịch biến trên
ℝ
![]()
![]()
![]()
![]()
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số nghịch biến trên
D
[
2
;
+
∞
)
. A. B. C. D.
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số ![]() nghịch biến trên
D
=
[
2
;
+
∞
)
.
nghịch biến trên
D
=
[
2
;
+
∞
)
.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số
y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
2...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng ( 0 ; 1 )
A. [ - 1 ; + ∞ )
B. ( - ∞ ; 0 ]
C. [ - 1 ; 0 ]
D. [ 0 ; 1 ]
Với tất cả các giá trị thực nào của tham số m thì hàm số
y
x
3
-
3
(
m
+
1
)
x
2
+
3
m
(
m
+
2...
Đọc tiếp
Với tất cả các giá trị thực nào của tham số m thì hàm số y = x 3 - 3 ( m + 1 ) x 2 + 3 m ( m + 2 ) x nghịch biến trên đoạn [0;1]?
A. - 1 ≤ m ≤ 0
B. - 1 < m < 0
C. m ≥ - 1
D. m ≤ 0
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên
ℝ
A. Không có m B.
-
1
≤
m
≤
-
1
2
C.
m
-
1
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số ![]() đồng biến trên
ℝ
đồng biến trên
ℝ
A. Không có m
B. - 1 ≤ m ≤ - 1 2
C. m < - 1 2
D. m > - 1
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y sinx+ cosx+ mx đồng biến trên
ℝ
A. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx+ cosx+ mx đồng biến trên ℝ
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên
ℝ
. A. B.
-
1
2
≤
m
≤
1
2
C.
-
3
m
≤
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số ![]() đồng biến trên
ℝ
.
đồng biến trên
ℝ
.
A. 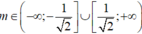
B. - 1 2 ≤ m ≤ 1 2
C. - 3 < m ≤ 1 2
D. 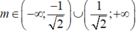
Tìm số các giá trị nguyên của tham số
m
∈
(
-
∞
;
+
∞
)
để hàm số
y
(
2
m
-
1
)
x
-
(
3
m
+...
Đọc tiếp
Tìm số các giá trị nguyên của tham số m ∈ ( - ∞ ; + ∞ ) để hàm số y = ( 2 m - 1 ) x - ( 3 m + 2 ) cos x nghịch biến trên ℝ .
A. 3
B. 4
C. 4014
D. 218
tìm các giá trị của m để hàm số sau
a) \(y=-x^3-\left(m+1\right)x^2+3\left(m+1\right)x\) nghịch biến trên R
b) \(y=-\dfrac{1}{3}x^3+mx^2-\left(2m+3\right)x\) nghịch biến trên R