Các câu hỏi tương tự
Tìm tất cả các giá trị của tham số a để phương trình sau có nghiệm duy nhất
a
log
3
x
3
+
4
log
3
x
8
+
a
+
1
0
A. a1. B. a-1. C. Không tồn tại a. D. a1.
Đọc tiếp
Tìm tất cả các giá trị của tham số a để phương trình sau có nghiệm duy nhất a log 3 x 3 + 4 log 3 x 8 + a + 1 = 0
A. a=1.
B. a<-1.
C. Không tồn tại a.
D. a<1.
Cho hàm số
y
ax
3
+
bx
2
+
cx
+
d
với
a
≠
0
có hai hoành độ cực trị là x1 và x3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) f(m) có đúng ba nghiệm phân biệt là: A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = ax 3 + bx 2 + cx + d với a ≠ 0 có hai hoành độ cực trị là x=1 và x=3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) = f(m) có đúng ba nghiệm phân biệt là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y
a
x
3
+
b
x
2
+
c
x
+
d
với a khác 0 có hai hoành độ cực trị là x1 và x3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) f(m) có đúng ba nghiệm phân biệt là:
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d với a khác 0 có hai hoành độ cực trị là x=1 và x=3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) = f(m) có đúng ba nghiệm phân biệt là:
![]()
![]()
![]()
![]()
Xác định giá trị của tham số m để phương trình x 3 + m x 2 + x - 5 = 0 có nghiệm dương
A. m = 5; B. m ∈ R;
C. m = -3; D. m < 0
Xác định giá trị của tham số m để phương trình x 3 + m x 2 + x - 5 = 0 có nghiệm dương
A. m = 5; B. m ∈ R;
C. m = -3; D. m < 0
Cho phương trình
m
.
l
n
2
(
x
+
1
)
-
(
x
+
2
-
m
)
l
n
(
x
+
1
)
-
x
-
2
0
(1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn
0...
Đọc tiếp
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Cho hàm số f(x) có đạo hàm liên tục trên
ℝ
và thỏa mãn f(x) 0,
∀
x
∈
ℝ
. Biết f(0) 1 và
f
(
x
)
(
6
x
-
3
x
2
)
f
(
x
)
.
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) m có ngh...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên ℝ và thỏa mãn f(x) > 0, ∀ x ∈ ℝ . Biết f(0) = 1 và f ' ( x ) = ( 6 x - 3 x 2 ) f ( x ) . Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.
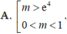
![]()
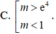
![]()
Cho bất phương trình
9
x
+
(
m
-
1
)
.
3
x
+
3
0
(
1
)
. Tìm tất cả các giá trị của tham số m để bất phương trình (1) nghiệm đúng
∀
x
1
A.
m
≥
-
3
2...
Đọc tiếp
Cho bất phương trình 9 x + ( m - 1 ) . 3 x + 3 > 0 ( 1 ) . Tìm tất cả các giá trị của tham số m để bất phương trình (1) nghiệm đúng ∀ x > 1
A. m ≥ - 3 2
B. m > - 3 2
C. m > 3 + 2 2
D. m ≥ 3 + 2 2
Tìm tất cả các giá trị của tham số thực m để phương trình
log
3
2
x
-
3
log
3
x
+
2
m
-
7
0
có hai nghiệm thực x1, x2 thỏa mãn (x1 + 3)(x2 + 3) 72. A.
m
61
2
B.
m...
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để phương trình log 3 2 x - 3 log 3 x + 2 m - 7 = 0 có hai nghiệm thực x1, x2 thỏa mãn (x1 + 3)(x2 + 3) = 72.
A. m = 61 2
B. m = 3
C. K h ô n g t ồ n t ạ i
D. m = 9 2




