Xét điểm M(x; y; z). Ta có: M cách đều hai mặt phẳng ( α ) và ( β )
⇔ d(M, ( α )) = d(M, ( β ))
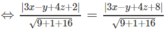
⇔ 3x – y + 4z + 5 = 0
Xét điểm M(x; y; z). Ta có: M cách đều hai mặt phẳng ( α ) và ( β )
⇔ d(M, ( α )) = d(M, ( β ))
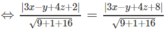
⇔ 3x – y + 4z + 5 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng Q 1 : 3 x - y + 4 z + 2 = 0 và Q 2 : 3 x - y + 4 z + 8 = 0 . Phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng Q 1 và Q 2 là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( Q 1 ) : 3x-y+4z+2=0 và ( Q 2 ) : 3x-y+4z+8=0 Phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng ( Q 1 ) và ( Q 2 ) là:
A. (P): 3x-y+4z+10=0
B. (P): 3x-y+4z+5=0
C. (P): 3x-y+4z-10=0
D. (P): 3x-y+4z-5=0
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng:
α : 3 x + ( m - 1 ) y + 4 z - 2 = 0 , β : n x + ( m + 2 ) y + 2 z + 4 = 0 ,
Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β).
A. m = - 3 , n = 1 2
B. m = 5 , n = 2 3
C. m = - 5 , n = 3 2
D. m = 5 , n = - 3 2
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng ( α ) : 3 x + ( m - 1 ) y + 4 z - 2 = 0 , ( β ) : n x + ( m + 2 ) y + 2 z + 4 = 0 . Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β)
A. m = - 5 ; n = 3 2
B. m = - 5 ; n = 5 2
C. m = - 3 ; n = 3 2
D. m = - 3 ; n = 5 2
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng ( α ) : 3 x + ( m - 1 ) y + 4 z - 2 = 0 , ( β ) : n x + ( m + 2 ) y + 2 z + 4 = 0 . Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β)
A. m = - 5 ; n = 3 2
B. m = - 5 ; n = 5 2
C. m = - 3 ; n = 3 2
D. m = - 3 ; n = 5 2
Tính khoảng cách từ điểm M(1; 2; 0) lần lượt đến các mặt phẳng sau: ( β ): 3x + 4z + 25 = 0
Trong không gian Oxyz cho mặt phẳng (P): 5x+my+4z+n=0 đi qua giao tuyến của hai mặt phẳng α : 3x-7y+z-3=0 và β : x-9y-2z+5=0. Tính m+n
A. 6
B. -16
C. -3
D. -4
Trong không gian Oxyz cho mặt phẳng (P): 5x+my+4z+n=0 đi qua giao tuyến của hai mặt phẳng (α): 3x-7y+z-3=0 và (β): x-9y-2z+5=0. Tính m+n.
A. 6.
B. -16.
C. -3.
D. -4.
Trong không gian Oxyz, tập hợp các điểm cách đều hai mặt phẳng (P): x + 3y - 4z + 1 = 0 và (Q): x + 3y - 4z + 7 = 0 là:
A. x + 3y - 4z + 8 = 0
B. x + 3y - 4z + 6 = 0
C. x + 3y - 4z + 4 = 0
D. x + 3y - 4z - 6 = 0