Các câu hỏi tương tự
Cho hàm số f(x) có đạo hàm trên khoảng
0
;
+
∞
và f(x)0,
∀
x
∈
0
;
+
∞
thỏa mãn
f
x
-
x
.
f
2
x
∀
x
∈
0
;...
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên khoảng 0 ; + ∞ và f(x)>0, ∀ x ∈ 0 ; + ∞ thỏa mãn f ' x = - x . f 2 x ∀ x ∈ 0 ; + ∞ , biết f 1 = 2 a + 3 và f 2 > 1 4 . Tổng tất cả các giá trị nguyên của a thỏa mãn là
A. -14.
B. 1.
C. 0.
D. -2.
Cho hàm số y f(x) có đạo hàm f(x)0,
∀
x
∈
1
;
2
thỏa mãn f(1) 1, f(2) 22/14 và
∫
1
2
f
x
3
x
4...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f'(x)>0, ∀ x ∈ 1 ; 2 thỏa mãn f(1) = 1, f(2) = 22/14 và ∫ 1 2 f ' x 3 x 4 d x = 7 375 . Tích phân ∫ 1 2 f x d x bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
tìm x, biết:
a. - 12 . ( x - 5) + 7 . ( 3 - x ) =5
b. 30 .( x+ 2 ) - 6 . ( x- 5) -24 .x = 100
c. ( x - 1 ) . ( x mũ 2 + 1) = 0
d. - 12 .( x-5) + 7 . (3- x) =5
Cho hàm số
f
(
x
)
e
x
2
+
1
(
e
x
-
e
-
x
)
Có bao nhiêu số nguyên dương m thỏa mãn bất phương trình
f
(
m...
Đọc tiếp
Cho hàm số f ( x ) = e x 2 + 1 ( e x - e - x ) Có bao nhiêu số nguyên dương m thỏa mãn bất phương trình f ( m - 7 ) + f ( 12 m + 1 ) ≤ 0
A. 4
B. 6.
C. 3.
D. 5.
Cho \(A=x^{1^{2^{3^{4^{5^{6^{7^{8^{9^{10^{11^{12^{13^{14^{15^{16^{17^{18^{19^{20^{21^{22^{.......}}}}}}}}}}}}}}}}}}}}}}},B=x^{\text{\pi}^{\pi^{\pi^{\pi^{\pi^{...^{...^{..}}}}}}}}\)
Tìm giá trị \(\left(2A-A\right)A-1\left(A+1\right)-B\)
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(1) 0
∫
0
1
f
(
x
)
2
d
x
7
,
∫
0
1
x
2
f
(
x
)
d...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(1) = 0 ∫ 0 1 f ' ( x ) 2 d x = 7 , ∫ 0 1 x 2 f ( x ) d x = 1 3 Tích phân ∫ 0 1 f ( x ) d x bằng:
A. 7/5
B. 1
C. 7/4
D. 4
Giá trị nhỏ nhất của hàm số f(x) = x +1/x trên nửa khoảng [2;+••] A:2 B:5/2 C:0 D:7/2
Cho hàm số
y
f
(
x
)
thỏa mãn
f
(
2
)
1
4
và
f
(
x
)
2
x
.
[
f
(
x
)
]
2
với
∀
x
∈
R
tính...
Đọc tiếp
Cho hàm số y = f ( x ) thỏa mãn f ( 2 ) = 1 4 và f ' ( x ) = 2 x . [ f ( x ) ] 2 với ∀ x ∈ R tính f ( 1 )
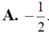
![]()
Tìm tất cả các giá trị của tham số thực m để phương trình
log
3
2
x
-
3
log
3
x
+
2
m
-
7
0
có hai nghiệm thực x1, x2 thỏa mãn (x1 + 3)(x2 + 3) 72. A.
m
61
2
B.
m...
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để phương trình log 3 2 x - 3 log 3 x + 2 m - 7 = 0 có hai nghiệm thực x1, x2 thỏa mãn (x1 + 3)(x2 + 3) = 72.
A. m = 61 2
B. m = 3
C. K h ô n g t ồ n t ạ i
D. m = 9 2