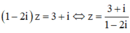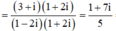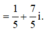Các câu hỏi tương tự
Trong mặt phẳng Oxy, gọi A là điểm biểu diễn số phức z thỏa mãn:left(1-2iright)z-dfrac{2-i}{1+i}left(3-iright)z . Tọa độ trung điểm I của OA làA: I left(dfrac{1}{20};dfrac{7}{20}right)B: I left(dfrac{1}{5};dfrac{7}{5}right)C:I left(dfrac{1}{10};dfrac{7}{10}right)D:I left(dfrac{1}{16};dfrac{7}{16}right)
Đọc tiếp
Trong mặt phẳng Oxy, gọi A là điểm biểu diễn số phức z thỏa mãn:\(\left(1-2i\right)z-\dfrac{2-i}{1+i}=\left(3-i\right)z\) . Tọa độ trung điểm I của OA là
A: I \(\left(\dfrac{1}{20};\dfrac{7}{20}\right)\)
B: I \(\left(\dfrac{1}{5};\dfrac{7}{5}\right)\)
C:I \(\left(\dfrac{1}{10};\dfrac{7}{10}\right)\)
D:I \(\left(\dfrac{1}{16};\dfrac{7}{16}\right)\)
Cho số phức z thỏa mãn điều kiện:
z
-
1
+
2
i
5
và
w
z
+
1
+
i
có môđun lớn nhất. Số phức z có môđun bằng: A.
2
5
B.
3
2
C.
6
D.
5
2
Đọc tiếp
Cho số phức z thỏa mãn điều kiện: z - 1 + 2 i = 5 và w = z + 1 + i có môđun lớn nhất. Số phức z có môđun bằng:
A. 2 5
B. 3 2
C. 6
D. 5 2
Cho số phức z thỏa mãn điều kiện:
z
-
1
+
2
i
5
và w z +1 +i có môđun lớn nhất. Số phức z có môđun bằng: A.
6
B.
3
2
C.
5
2
D.
2
5
Đọc tiếp
Cho số phức z thỏa mãn điều kiện: z - 1 + 2 i = 5 và w = z +1 +i có môđun lớn nhất. Số phức z có môđun bằng:
A. 6
B. 3 2
C. 5 2
D. 2 5
Tìm số phức z thỏa mãn (1 + i)z + (2 - 3i)(1 + 2i) 7 + 3i. A. B. C. D.
Đọc tiếp
Tìm số phức z thỏa mãn (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i.
A. ![]()
B. ![]()
C. ![]()
D. 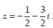
Cho số phức z thỏa mãn
(
2
+
3
i
)
z
-
(
1
+
2
i
)
z
¯
7
-
i
. Tìm mô đun của z. A.
z
1 B.
z...
Đọc tiếp
Cho số phức z thỏa mãn ( 2 + 3 i ) z - ( 1 + 2 i ) z ¯ = 7 - i . Tìm mô đun của z.
A. z =1
B. z =2
C. z = 3
D. z = 5
Cho các số phức w,z thỏa mãn
w
+
i
3
5
5
và 5w(2+i)(z-4). Giá trị lớn nhất của biểu thức
P
z
-
1
-...
Đọc tiếp
Cho các số phức w,z thỏa mãn w + i = 3 5 5 và 5w=(2+i)(z-4).
Giá trị lớn nhất của biểu thức P = z - 1 - 2 i + z - 5 - 2 i bằng
A. 6 7
B. 4 + 2 13
C. 2 53
D. 4 13
Cho các số phức w, z thỏa mãn
w
+
i
3
5
5
và
5
w
(
2
+
i
)
(
z
-
4
)
. Giá trị lớn nhất của biểu thức
P
z
-
1
-...
Đọc tiếp
Cho các số phức w, z thỏa mãn w + i = 3 5 5 và 5 w = ( 2 + i ) ( z - 4 ) . Giá trị lớn nhất của biểu thức P = z - 1 - 2 i + z - 5 - 2 i bằng
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn
z
-
1
2
-
i
+
i
5
. Biết rằng tập hợp biểu diễn số phức w (1-i)z + 2i có dạng...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 2 - i + i = 5 . Biết rằng tập hợp biểu diễn số phức w = (1-i)z + 2i có dạng ( x + 2 ) 2 + y 2 = k Tìm k.
A. k = 92
B. k = 92
C. k = 50
D. k = 96
Tìm số phức z thỏa mãn:
(
2
+
i
)
z
(
3
-
2
i
)
z
¯
-
4
(
1
-
i
)
Đọc tiếp
Tìm số phức z thỏa mãn: ( 2 + i ) z = ( 3 - 2 i ) z ¯ - 4 ( 1 - i )
![]()
![]()
![]()
![]()
Tìm phần thực a của số phức z thỏa mãn (1 + i) 2( 2 - i) z 8 + i + (1 + 2i) z. A. a 2. B. a -3. C. a -2. D. a 3.
Đọc tiếp
Tìm phần thực a của số phức z thỏa mãn (1 + i) 2( 2 - i) z = 8 + i + (1 + 2i) z.
A. a = 2.
B. a = -3.
C. a = -2.
D. a = 3.