Đáp án D
Phương pháp:
Giải phương trình hoành độ giao điểm.
Cách giải:
![]()
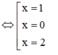
Vậy đồ thị hàm số y = (x - 1)(x2 - 2x) cắt trục hoành tại 3 điểm.
Đáp án D
Phương pháp:
Giải phương trình hoành độ giao điểm.
Cách giải:
![]()
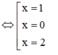
Vậy đồ thị hàm số y = (x - 1)(x2 - 2x) cắt trục hoành tại 3 điểm.
Số giao điểm của đồ thị hàm số y = (x − 3)( x 2 + x + 4) với trục hoành là:
A. 2; B. 3;
C. 0; D. 1.
Số giao điểm của đồ thị hàm số y = (x − 3)( x 2 + x + 4) với trục hoành là:
A. 2; B. 3;
C. 0; D. 1
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Tìm số giao điểm của đồ thị hàm số y = (x – 2)(x2 + x + 1) và trục hoành.
A. 1
B. 0
C. 2
D. 3
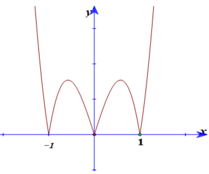
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 7 15
B. 8 15
C. 14 15
D. 16 15
Xét các khẳng định sau:
(1) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 1 điểm chung.
(2) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 và f(0).f(1)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 2 điểm chung.
Phát biểu nào sau đây đúng?
A. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() sai.
sai.
B. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() đúng.
đúng.
C. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() sai.
sai.
D. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() đúng.
đúng.
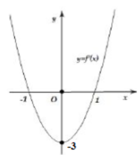
Cho hàm số y=f(x)= a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ R , a khác 0) có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y= f ' ( x ) cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giời hạn bởi đồ thị (C) và trục hoành xung quanh trục hoành Ox
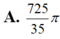
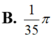
![]()
![]()
Số giao điểm của đồ thị hàm số y = x - 1 1 3 x 2 - 2 x + 3 với trục hoành là
A. 3
B. 4
C. 1
D. 5
Viết phương trình tiếp tuyến của đồ thị hàm số:
\(y=\dfrac{-x+2}{x+1}\)
a, Tại giao điểm của đồ thị vs trục hoành
b, Tại giao điểm của đồ thị vs trục tung
c, Hệ số góc \(k=-3\)