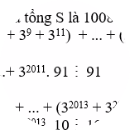\(\left(3n+8\right)⋮\left(n+2\right)\\ \Leftrightarrow\left(3n+6+2\right)⋮\left(n+2\right)\\ \Leftrightarrow\left[3\left(n+2\right)+2\right]⋮\left(n+2\right)\)
Vì \(3\left(n+2\right)⋮\left(n+2\right)\Rightarrow2⋮\left(n+2\right)\Rightarrow n+2\inƯ\left(2\right)\)
Ta có bảng:
| n+2 | -2 | -1 | 1 | 2 |
| n | -4 | -3 | -1 | 0 |
Vậy \(n\in\left\{-4;-3;-1;0\right\}\)
\(3n+8⋮n+2\)
\(n+2⋮n+2\Rightarrow3\left(n+2\right)⋮n+2\Rightarrow3n+6⋮n+2\)
\(\Rightarrow\left(3n+8\right)-\left(3n+6\right)⋮n+2\)
\(\Rightarrow3n+8-3n-6⋮n+2\)
\(\Rightarrow\left(3n-3n\right)+\left(8-6\right)⋮n+2\)
\(\Rightarrow2⋮n+2\)
\(\Rightarrow n+2\) là ước của 2
\(\Rightarrow n+2\in\left\{1;-1;2;-2\right\}\)
ta có bảng
n+2 1 -1 2 -2
n -1 -3 0 -4
rồi tự kl đi