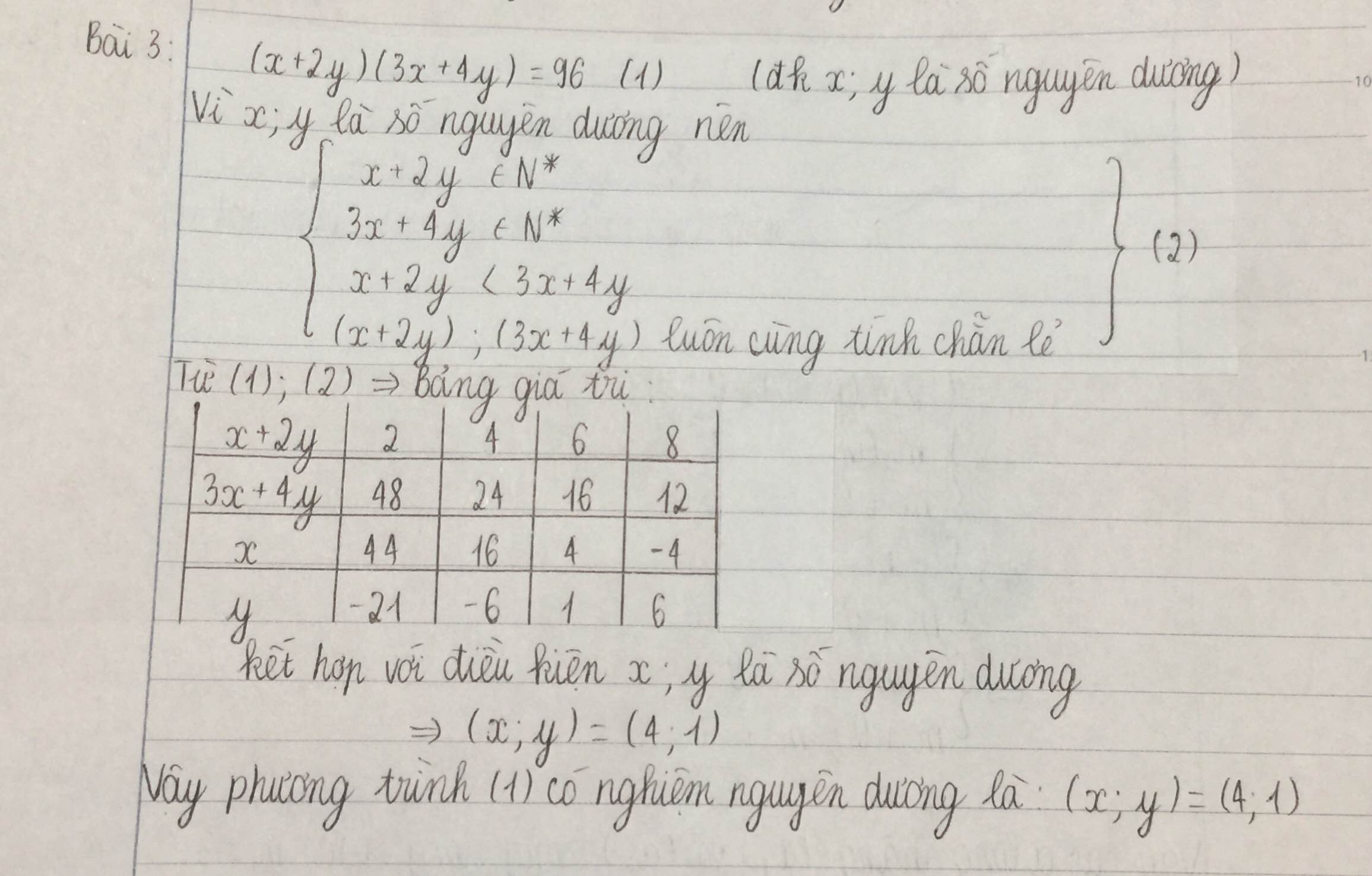Question

Tìm nghiệm nguyên dương của phương trình $(x+2y)(3x+4y)=96$.

Answer 1

Ta có: \(\left(x+2y\right)\left(3x+4y\right)=96\) ( x,y nguyên)

Lại có: \(3x+4y-\left(x+2y\right)=2x+2y\) ( chẵn)

=> 3x+4y , x+2y cùng chẵn hoặc cùng lẻ ( 1)

Mà (x+2y)(3x+4y)=96 chẵn 

=> 3x+4y, x+2y cùng chẵn hoặc là một chẵn 1 lẻ ( 2)

Từ (1) và (2) => 3x+4y, x+2y cùng chẵn

Ta có bảng sau: 

3x+4y	48	2	24	4	16	6	12	8
x+2y	2	48	4	24	6	16	8	12
x	44	-94	16	-44	4	-26	-4	-16
y	-21	71	-6	34	1	21	6	14

Vậy ...

Answer 2

x=4; y=1

Answer 3

ta có 96=6.16

xy là các số nguyên nên 3x+4y>x+2y

do đó xy là các nghiệm nguyên dương của phương trình khi

3x+4y+16

x+2y=6

giẢI hệ ta được x=4 y=1

vậy nghiệm của phương trình là (4,1)

Answer 4

ta có 96=6.16

xy là các số nguyên nên 3x+4y>x+2y

do đó xy là nghiệm nguyên dương của pt khi :

3x+4y=16

x+2y=6

=> x=4

y=1

vậy nghiệm pt là (4,1)

 

 

Answer 5

E ko biết cách trình bày!

Answer 6

3x^2 +10xy + 8y^2 = 96 
<=> 3x^2 + 6 xy + 4xy +8y^2=96 
<=> 3x(x+2y) + 4y(x+2y) = 96 
<=> (3x+4y)(x+2y) = 96 
Mặt khác, ta thấy x+2y đồng tính chẵn lẻ với x, 3x+4y = x+2(x+2y) đồng tính chẵn lẻ với x, do đó cặp nghiệm (3x+4y, x+2y) sẽ đồng tính chẵn lẻ. Dễ dàng thấy 96 = 2^5 *3, do đó các cặp nghiệm có khả năng có nghiệm chỉ là các cặp nghiệm chẵn. 
Các cặp nghiệm chẵn (3x+4y, x+2y) sẽ là (2,48), (4,24), (6,16), (8,12), (12, 8), (16,6), (24,4), (48,2) và các cặp nghiệm âm tương ứng 

Answer 7

96=6.16 Xy là số nguyên nên 3x+4y>x+2y =>xy là là n° nguyên dương của ptrinh khi 3x+4y+16 X+2y=6 (Giải hệ) ............... X=4; y=1 Vậy n° ptrinh là 4,1

Answer 8

X,y là các số nguyên nên 3x + 4y > x+2y do đó x,y là các nghiệm dương của pt khi:
Pt1 3x+4y=16
Pt2 x+2y=6
Suy ra x=4
Y=1

Answer 9

{44;-21} ; {-94;71} ; {16;-6}; {-44;34};{4;1}Ư ; {-26;21} ; {-4;6} ; {-16;14}

Answer 10

x=4;y=1

Answer 11

Nghiệm của phương trình là x=4 ;y=1

Answer 12

Ta có: $\left(x+2y\right)\left(3x+4y\right)=96$ ( x,y nguyên)

Lại có: $3x+4y-\left(x+2y\right)=2x+2y$ ( chẵn)

=> 3x+4y , x+2y cùng chẵn hoặc cùng lẻ ( 1)

Mà (x+2y)(3x+4y)=96 chẵn 

=> 3x+4y, x+2y cùng chẵn hoặc là một chẵn 1 lẻ ( 2)

Từ (1) và (2) => 3x+4y, x+2y cùng chẵn

Ta có bảng sau: 

3x+4y	48	2	24	4	16	6	12	8
x+2y	2	48	4	24	6	16	8	12
x	44	-94	16	-44	4	-26	-4	-16
y	-21	71	-6	34	1	21	6	14

Vậy ...

Answer 13

S={1, 4}

Answer 14

 

Answer 15

 

Answer 16

 vậy nghiệm nguyên dương của phương trình đã cho là ...

Answer 17

 

Answer 18

  

Answer 19

Hai số $x+2y$ và $3x+4y$ có tích là số chẵn và hiệu là số chẵn nên cả hai số đều chẵn.

Chú ý rằng $3x+4y>x+2y$ với mọi $x,$ $y$ nguyên dương.

Answer 20

Hai số $x+2y$ và $3x+4y$ có tích là số chẵn và hiệu là số chẵn nên cả hai số đều chẵn.

Chú ý rằng $3x+4y>x+2y$ với mọi $x,$ $y$ nguyên dương.

Answer 21

Hai số $x+2y$ và $3x+4y$ có tích là số chẵn và hiệu là số chẵn 

$chú\; ý\; rằng\; 3x+4y>x+2y$ với mọi $x,$ y

$y$ nguyên dương. nên cả hai số đều chẵn

Answer 22

Hai số $x+2y$ có tích là số chẵn và hiệu là số chẵn nên cả hai số đều chẵn.

Chú ý rằng $3x+4y>x+2y$ $y$ nguyên dương.

Answer 23

  

Answer 24

 

Answer 25

 

Answer 26

x=4 ; y=1

Answer 27

x=4;y=1

Answer 28

 

Answer 29

Ta có: $\left(x+2y\right)\left(3x+4y\right)=96$ ( x,y nguyên)

Lại có: $3x+4y-\left(x+2y\right)=2x+2y$ ( chẵn)

=> 3x+4y , x+2y cùng chẵn hoặc cùng lẻ ( 1)

Mà (x+2y)(3x+4y)=96 chẵn 

=> 3x+4y, x+2y cùng chẵn hoặc là một chẵn 1 lẻ ( 2)

Từ (1) và (2) => 3x+4y, x+2y cùng chẵn

Ta có bảng sau: 

3x+4y	48	2	24	4	16	6	12	8
x+2y	2	48	4	24	6	16	8	12
x	44	-94	16	-44	4	-26	-4	-16
y	-21	71	-6	34	1	21	6	14

Answer 30