Đáp án C
Phương pháp:
Giải phương trình logarit cơ bản:
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
17 tháng 12 2023 lúc 20:24
Câu 11: Nghiệm của phương trình \(\log^2_{\frac{1}{2}} (x-2)-(2-x)\log_{2} (x-2)+3(x-5)=0\) là?
Tìm tập nghiệm của bất phương trình: 2 2 x 8 > 1
A. x > 3/2 B. x < 3/2
C. x > 2/3 D. x < 2/3
Tìm số nghiệm nguyên của bất phương trình
log
5
2
(
3
x
-
2
)
log
2
(
4
-
x...
Đọc tiếp
Tìm số nghiệm nguyên của bất phương trình log 5 2 ( 3 x - 2 ) log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Tìm tập nghiệm của bất phương trình:
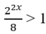
A. x > 3/2 B. x < 3/2
B. x > 2/3 D. x < 2/3
Tìm tập nghiệm của bất phương trình log ( x - 21 ) < 2 - log x
A. (-4; 25)
B. (0; 25)
C. (21; 25)
D. (25; +∞)
Tìm tập hợp nghiệm của phương trình:
1
25
.
5
x
+
x
3
A. {2;
log
5
3
} B. {5;
log
5
2
}C. {...
Đọc tiếp
Tìm tập hợp nghiệm của phương trình: 1 25 . 5 x + x = 3
A. {2; log 5 3 } B. {5; log 5 2 }
C. { log 5 3 } D. {2}
Nghiệm của phương trình
log
4
2
log
3
1
+
log
2
1
+...
Đọc tiếp
Nghiệm của phương trình log 4 2 log 3 1 + log 2 1 + 3 log 2 x = 1/2 là
A. x = 1 B. x = 2
C. x = 3 D. x = 0
Nghiệm của phương trình log 4 { 2 log 3 [ 1 + log 2 ( 1 + 3 log 2 x ) ] } = 1/2 là
A. x = 1 B. x = 2
C. x = 3 D. x = 0
Phương trình log 3 x + log 9 x = 3/2 có nghiệm là
A. x = 1 B. x = 1/2
C. x = 1/3 D. x = 3
Phương trình log 3 x + log 9 x = 3/2 có nghiệm là
A. x = 1 B. x = 1/2
C. x = 1/3 D. x = 3