Vẽ đồ thị hàm số y = x 3 + 3 x 2 – 9 x + 2 (C)
Giữ phần đồ thị (C) phía trên trục Ox, lấy đối xứng phần đồ thị (C) dưới trục Ox qua trục Ox.
Bỏ phần đồ thị dưới trục Ox ta được đồ thị y = x 3 + 3 x 2 – 9 x + 2 .
Dựa vào đồ thị ta có đáp án A.
Vẽ đồ thị hàm số y = x 3 + 3 x 2 – 9 x + 2 (C)
Giữ phần đồ thị (C) phía trên trục Ox, lấy đối xứng phần đồ thị (C) dưới trục Ox qua trục Ox.
Bỏ phần đồ thị dưới trục Ox ta được đồ thị y = x 3 + 3 x 2 – 9 x + 2 .
Dựa vào đồ thị ta có đáp án A.
Giả sử phương trình l o g 2 2 x - ( m - 2 ) l o g 2 x + 2 m = 0 có hai nghiệm thực phân biệt x 1 , x 2 thỏa mãn x 1 + x 2 = 6 . Giá trị của biểu thức x 1 - x 2 là
A.3
B.8
C.2
D.4
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
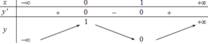
Khi đó phương trình f(x) +1=m có ba nghiệm thực phân biệt khi và chỉ khi
A. 1<m<2
B. 1 ≤ m ≤ 2
C. 0 ≤ m ≤ 1
D. 0<m<1
cho (Cm) y=2x^3-3(2m+1)x^2+6m(m+1)x-2m^3
Tìm m để (Cm) cắt trục Ox tại 3 điểm phân biệt
Cho bất phương trình x 4 + x 2 + m 3 - 2 x 2 + 1 3 + x 2 x 2 - 1 > 1 - m . Tìm tất cả các giá trị thực của tham số m để bất phương trình trên nghiệm đúng ∀ x > 1 .
![]()
![]()

![]()
Cho hàm số f(x) = x3-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình x 3 - 3 x 2 + 2 = m có nhiều nghiệm thực nhất
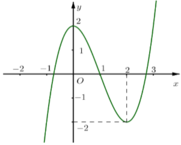
A. m> -2
B. m> 0
C. -2< m< 2.
D. m< 2.
Cho hàm số y = f(x) thỏa mãn f(-2) = -2, f(2) = 2 và có bảng biến thiên như hình bên
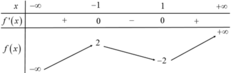
Có bao nhiêu số tự nhiên m thỏa mãn bất phương trình f - f x ≥ ≥ m có nghiệm thuộc đoạn [-1;1]?
A. 1.
B. 2.
C. 3.
D. 4.
Số nghiệm của phương trình | x 3 | - 12 | x | = m (với -1 < m < 0 ) là
A. 1
B. 2
C. 3
D. 4
Cho hàm số f(x)=x^2-4x+3. Có bao nhieu giá trị nguyên của tham số m để phương trình f^2(/x/)-(m-6)f(/x/)-m+5=0 có 6 nghiệm phân biệt
Tìm tập nghiệm của phương trình l o g ( x + 3 ) + l o g ( x - 1 ) = l o g ( x 2 - 2 x - 3 )
A. ∅
B. {0}
C. R
D. (1; +∞)