* Nếu m = 0 thì y = x nên hàm số đã cho không có tiệm cận ngang.
* Nếu m = 1 thì y = 1 nên hàm số không có tiệm cận ngang.
* Nếu m = -1 thì y = -1 nên hàm số không có tiệm cận ngang.
Vậy để hàm số đã cho có tiệm cận ngang thì m ≠ 0 và m ≠ ±1;
Chọn D
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x - 2 x 2 - 4 là:
A. 0.
B. 1.
C. 2.
D. 3.
Đồ thị hàm số y = x 2 + x - x 2 + 1 có đường tiệm cận ngang có phương trình là
A. y = 1
B. y = 0
C. y = 1 2
D. y = ± 1 2
Đồ thị của hàm số nào dưới đây không có đường tiệm cận ?
A. 
B.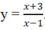 
C. y = x4 – 2016
D.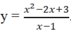 
Cho hàm số y = x 4 2 - 2 m 2 x 2 + 2 . Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng 64 15 là
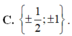
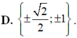
Tìm m để đồ thị hàm số y = x 3 + 3 x 2 + m x + 2 m cắt đường thẳng y = -x + 2 tại 3 điểm.
A. m > 5 4
B. m > 1
C. m < 5 4 và m ≠ - 1
D. - 1 < m < 5 4
Tìm m để đồ thị hàm số y = x 4 - 2 m 2 x 2 + 1 có ba cực trị tạo thành tam giác vuông
A. m = ± 1
B. m = ± 2
C. m = 3
D. Đáp án khác
Tìm m để đồ thị hàm số y = x 4 - 2 m 2 x 2 + 1 có ba cực trị tạo thành tam giác vuông
A. m = ± 1
B. m = ± 2
C. m = 3
D. Đáp án khác
Tìm tất cả các giá trị của tham số m sao cho đường thẳng y= 2m-1 cắt đồ thị hàm số y = x 3 - 3 x + 1 tại 4 điểm phân biệt
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. 0 < m < 1
D. m < 0
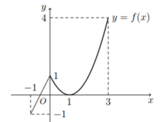
Cho hàm số f(x) liên tục trên [-1;3] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên [-1;3]. Tính M - m.
A. 3
B. 4
C. 5
D. 1
