Chọn A.
( Sử dụng công thức giải nhanh)
Áp dụng công thức giải nhanh, ta có phương trình đi qua hai điểm cực trị cần lập là
với 
Suy ra:
hay
Do A và B đối xứng nhau qua đường thẳng (hay 
)
Suy ra 
. Do bài toán chỉ có một đáp số nên 
thỏa mãn
Tìm m để đồ thị hàm số 
có hai điểm cực trị A và B đối xứng nhau qua đường thẳng 
A. 
B. 
C. 
D. 
Cho hàm số y= -x3+3mx2-3m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị đối xứng với nhau qua đường thẳng d: x+8y-74=0.
A. m=1
B. m=- 2
C. m= -1
D. m=1
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 m x 2 + 4 m 3 có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng ( d ) : y = x .
A. m = 2 2
B. m = - 2 2
C. m = 0 h o ặ c m = 2 2 .
D. m = ± 2 2
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y= x3- 3mx2+ 4m3 có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng x- y=0.
A. m = 2 2
B. m = - 2 2
C. m=0 hoặc m = 2 2
D. m = ± 2 2
Với giá trị nào của m, đồ thị hàm số y = x 3 + 3 x 2 + m 2 x + m có hai điểm cực trị đối xứng qua đường thẳng: y = 1 2 x - 5 2
A. m = 0
B. m = 1
C. m = -1
D. Không tồn tại
Đồ thị hàm số y = - x 3 + 3 m x 2 - 3 m - 1 có cực đại và cực tiểu đối xứng nhau qua đường thẳng d : x + 8 y - 74 = 0 khi m bằng.
A.1
B.-2
C.-1
D.2
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1)
a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.
b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m = 0
d) Xác định k để (C) cắt đường thẳng y = kx tại ba điểm phân biệt.
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 + m x 2 + 7 x + 3 có đường thẳng đi qua điểm cực đại và điểm cực tiểu vuông góc với đường thẳng có phương trình : y = 3 x ( d )
A. m = ± 45 2
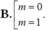
C. m = 2
D. m = ± 47 2
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.
B.
C.
D. 
