\(A=x-\sqrt{x}\) \(\left(ĐKXĐ:x\ge0\right)\)
\(A=x-2.\sqrt{x}.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\)
\(A=\left(x-\frac{1}{2}\right)^2\) \(-\frac{1}{4}\)
Có \(\left(x-\frac{1}{2^2}\right)\ge0\forall x\ge0\)
\(\left(x-\frac{1}{2}\right)^2\) - 1/4 >= \(\frac{-1}{4}\)mọi x>=0
Dấu = sảy ra \(\Leftrightarrow\) x- \(\frac{1}{2}\) = 0
\(\Leftrightarrow\) x = 1 / 2 ( t/m )
vậy A đạt GTNN là -1/4 tại x = 1/2
Tớ nhầm nhé \(x\) từ dòng thứ 3 xuống pahir thay =\(\sqrt{x}\)
A=\(x-\sqrt{x}\) ( ĐKXĐ x >=0 )
= \(x-2.\sqrt{x}.\frac{1}{2}\) \(+\frac{1}{4}-\frac{1}{4}\)
= \(\left(\sqrt{x}-\frac{1}{2}\right)^2\) - \(\frac{1}{4}\)
Có \(\left(\sqrt{x}-\frac{1}{2}\right)^2\) \(\ge0\forall x\ge0\)
\(\Rightarrow\left(\sqrt{x}-\frac{1}{2}\right)^2\) \(-\frac{1}{4}\ge\frac{-1}{4}\forall x\) >= 0
dấu = sảy ra \(\Leftrightarrow\sqrt{x}-\frac{1}{2}\)= 0 \(\Leftrightarrow\) x = \(\frac{1}{4}\) ( t/m )
Vậy A đạt GTNN là \(\frac{-1}{4}\) tại x= \(\frac{1}{4}\)
Vừa nãy tớ làm sai
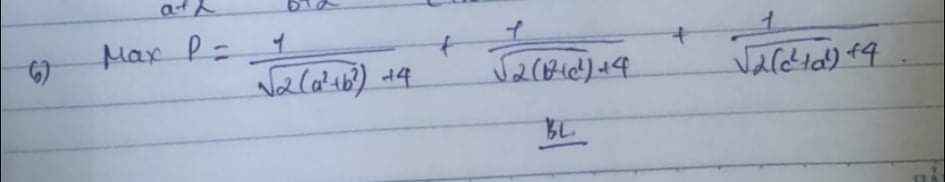mọi người giúp em với ạ😁😁😁
