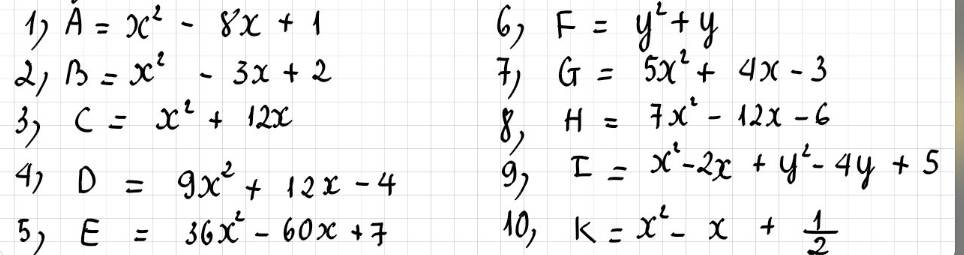+ \(A=x^2+2x\cdot\frac{1}{2}+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\forall x\)
Dấu "=" \(\Leftrightarrow\left(x+\frac{1}{2}\right)^2=0\Leftrightarrow x=-\frac{1}{2}\)
Vậy Min \(A=\frac{3}{4}\)\(\Leftrightarrow x=-\frac{1}{2}\)
+ \(B=x^2-3x=x^2-2x\cdot\frac{3}{2}+\frac{9}{4}-\frac{9}{4}\)
\(=\left(x-\frac{3}{2}\right)^2-\frac{9}{4}\ge-\frac{9}{4}\forall x\)
Min \(B=-\frac{9}{4}\Leftrightarrow x=\frac{3}{2}\)