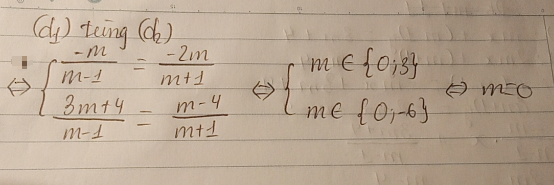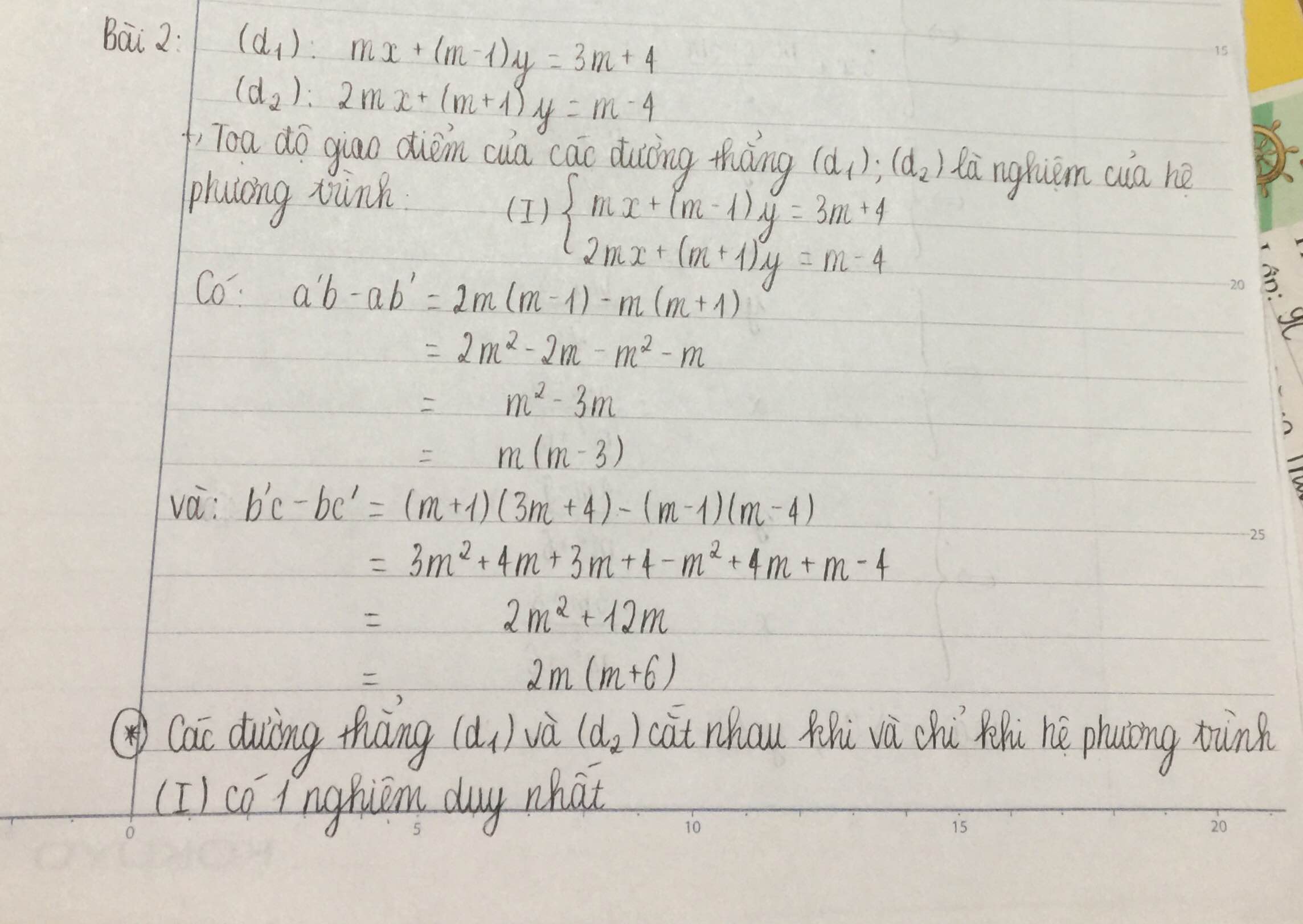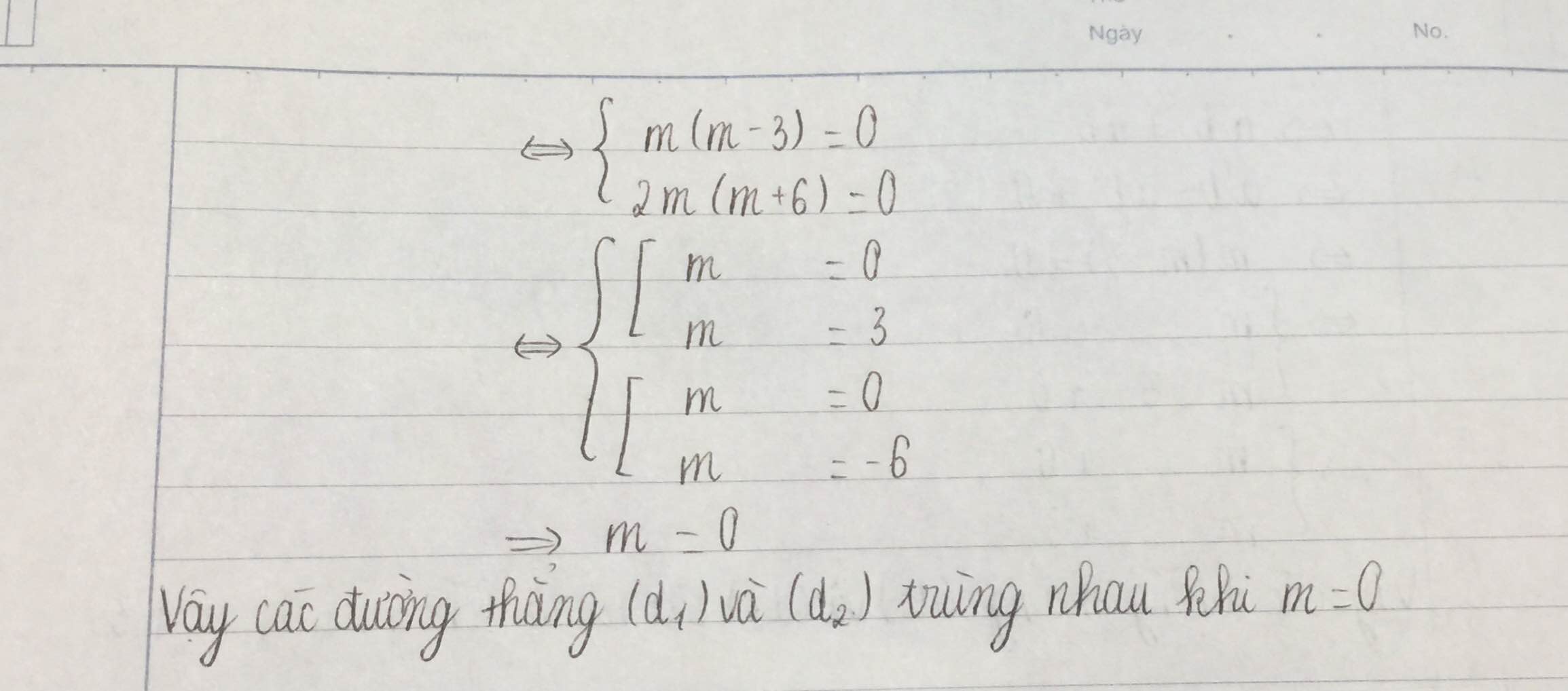Ta có: \(\hept{\begin{cases}\left(d_1\right):mx+\left(m-1\right)y=3m+4\\\left(d_2\right):2mx+\left(m+1\right)y=m-4\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(d_1\right):mx-3m-4=\left(1-m\right)y\\\left(d_2\right):2mx+4-m=-\left(m+1\right)y\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(d_1\right):\frac{m}{1-m}x-\frac{3m+4}{1-m}=y\\\left(d_2\right):-\frac{2m}{m+1}x+\frac{m-4}{m+1}=y\end{cases}}\) khi đó ta có:
Để (d1) // (d2) thì: \(\hept{\begin{cases}\frac{m}{m-1}=\frac{2m}{m+1}\\\frac{3m+4}{m-1}\ne\frac{m-4}{m+1}\end{cases}}\Rightarrow m=3\)
Đề (d1) cắt (d2) thì: \(\frac{m}{m-1}\ne\frac{2m}{m+1}\Rightarrow m\ne\left\{0;3\right\}\)
Để (d1) trùng (d2) thì: \(\hept{\begin{cases}\frac{m}{m-1}=\frac{2m}{m+1}\\\frac{3m+4}{m-1}=\frac{m-4}{m+1}\end{cases}}\Rightarrow m=0\)
Để(d1)//(d2)\(\Rightarrow m\text{=}3\)
Để(d1)cắt(d2)\(\Rightarrow m\ne\left(0;3\right)\)
Để(d1)trùng(d2)\(\Rightarrow m\text{=}0\)
để (d1) // (d2)=> m=3
để (d1) cắt (d2)=>m#(0,3)
để (d1) trùng (d2) => m=0
Để d1 và d2 trùng nhau thì a=a'b=b'=>m=2
Để d1 và d2 cắt nhau thì a khác a'=>m khác 2
Để d1 và d2 song song thì a=a'b khác b'=>m=2
Để d1 và d2 trùng nhau thì a=a'b=b'=>m=2
Để d1 và d2 cắt nhau thì a khác a'=>m khác 2
Để d1 và d2 song song thì a=a'b khác b'=>m=2
Cắt nhau : m khác 3 ; m khác 0
Song song : m = 0 ; m = 3
Trùng nhau : m= 0; m= -6 ; m= 3
song song khi m=-3
cắt nhau khi m khác 0 và m khác 3
trùng nhau khi m=0
Xét hiệu:
Ta có: .
Cắt nhau m khác 3;m khác 0
Song song m=-3
trùng nhau m=0
cắt nhau khi m khác 0,3
song song khi m=3
trùng nhau khi m=0
$\left.\begin{matrix} \text{AC là tiếp tuyến của đường tròn}\\\text{CD là tiếp tuyến của đường tròn}\\ AC\cap CD={C} \end{matrix}\right\} \Rightarrow \text{ AC=CM; OC là phân giác góc }\widehat{AOE}$
Để hàm số y = kx + m - 2 là hàm số bậc nhất khi k ≠ 0
Để hàm số y = (5 - k)x + (4 - m) là hàm số bậc nhất khi 5 - k ≠ 0 ⇔ k ≠ 5
a, Để đồ thị của hai hàm số trùng nhau
Vậy với ; m = 3 thì đồ thị của hai hàm số trùng nhau
b, Để đồ thị của hai hàm số song song với nhau
Vậy với ; m ≠ 3 thì đồ thị của hai hàm số song song với nhau
c, Để đồ thị của hai hàm số cắt nhau ⇔ k ≠ 5 - k ⇔ 2k ≠ 5 ⇔
Vậy với thì hai đồ thị hàm số cắt nhau
Xét hiệu:
Ta có: .
Xét hiệu:
Ta có: .
























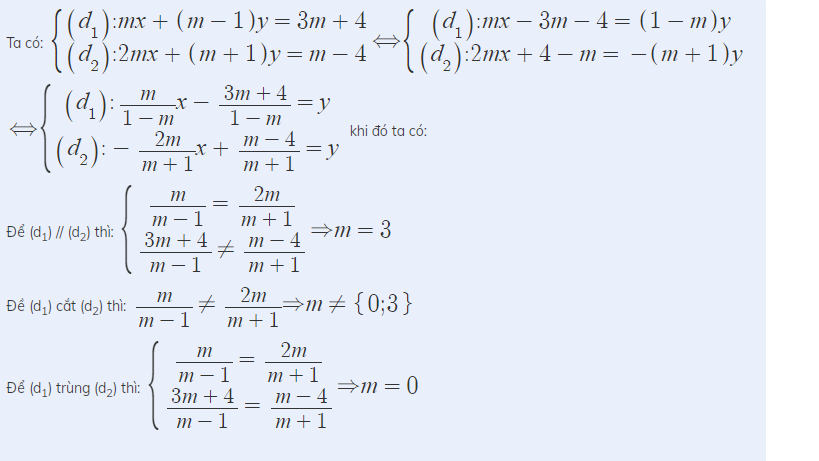

.png)