Các câu hỏi tương tự
Biết diện tích hình phẳng giới hạn bởi đường cong yf(x), y0, x2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong yf(2x), trục hoành Ox và hai đường thẳng x0, xa bằng:
Đọc tiếp
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
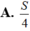
![]()
![]()
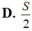
Diện tích hình phẳng giới hạn bởi đường cong
y
a
x
(a0), trục hoành và đường thẳng xa bằng
k
a
2
,
(
k
∈
ℝ
)
. Tính giá trị của tham số k.
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y = a x (a>0), trục hoành và đường thẳng x=a bằng k a 2 , ( k ∈ ℝ ) . Tính giá trị của tham số k.
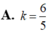
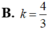
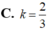
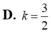
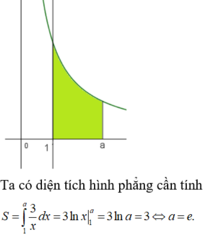
Với giá trị nào của a để diện tích S của hình phẳng giới hạn bởi(C)
y
x
2
-
2
x
x
-
1
, đường tiệm cận xiên của (C) và hai đường thẳng xa; x2a (a1) bằng ln3? A. a 1 B. a 2 C. a 3 D. a 4
Đọc tiếp
Với giá trị nào của a để diện tích S của hình phẳng giới hạn bởi(C) y = x 2 - 2 x x - 1 , đường tiệm cận xiên của (C) và hai đường thẳng x=a; x=2a (a>1) bằng ln3?
A. a = 1
B. a = 2
C. a = 3
D. a = 4
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình
y
x
2
-
4
x
+
3
và đường thẳng
y
x
+
3
(phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình y = x 2 - 4 x + 3 và đường thẳng y = x + 3 (phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng
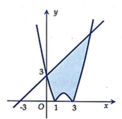
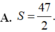
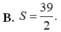
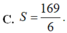
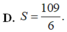
Cho hàm số liên tục trên [a;b] Diện tích hình phẳng S giới hạn bởi đường cong y f(x) trục hoành và các đường thẳng xa; xb; (ab) được xác định bởi công thức nào sau đây
Đọc tiếp
Cho hàm số liên tục trên [a;b] Diện tích hình phẳng S giới hạn bởi đường cong y = f(x) trục hoành và các đường thẳng x=a; x=b; (a<b) được xác định bởi công thức nào sau đây
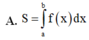
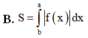

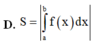
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình
y
x
2
−
4
x
+
3
và đường thẳng yx+3 (phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng (H) A.
S
47
2
.
B.
S
39
2...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình
y
=
x
2
−
4
x
+
3
và đường thẳng y=x+3 (phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng (H)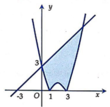
A. S = 47 2 .
B. S = 39 2 .
C. S = 169 2 .
D. S = 109 2 .
Diện tích hình phẳng giới hạn bởi các đường thẳng
y
-
x
,
n
ế
u
x
≤
1
x
-
2...
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường thẳng y = - x , n ế u x ≤ 1 x - 2 , n ế u x > 1 và y = 10 3 x - x 2 là a/b . Khi đó a + 2b bằng
A. 16
B. 15
C. 17
D. 18
Với giá trị nào của a để diện tích S của hình phẳng giới hạn bởi
C
:
y
x
2
−
2
x
x
−
1
, đường tiệm cận xiên của (C) và hai đường thẳng
x
a
,
x
2
a
a...
Đọc tiếp
Với giá trị nào của a để diện tích S của hình phẳng giới hạn bởi C : y = x 2 − 2 x x − 1 , đường tiệm cận xiên của (C) và hai đường thẳng x = a , x = 2 a a > 1 bằng ln3
A. a=1
B. a=2
C. a=3
D. a=4
Diện tích hình phẳng giới hạn bởi các đường
y
e
2
x
+
1
, trục hoành, đường thẳng x 1 và đường thẳng x 2 là
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường y = e 2 x + 1 , trục hoành, đường thẳng x = 1 và đường thẳng x = 2 là
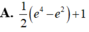
![]()
![]()
![]()